Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề thi thử học kì I lớp 8 (đề số 1) - Phần tự luận SVIP
Câu 7. ( 1,0 điểm): Tìm $x$, biết:
a) $3(x+2)-2=10$.
b) $x^2-5 x+6=0$.
Hướng dẫn giải:
a) $3(x+2)-2=10 \Leftrightarrow 3 x+6-2=10$
$\Leftrightarrow 3 x=6 \Leftrightarrow x=2$.
Vậy $x=2$.
b) $x^2-5 x+6=0 \Leftrightarrow x^2-2 x-3 x+6=0$
$\Leftrightarrow x(x-2)-3(x-2)=0 \Leftrightarrow(x-2)(x-3)=0 $
$\Leftrightarrow\left[\begin{aligned} &x - 2 = 0\\ &x - 3 = 0\\ \end{aligned} \Leftrightarrow \left[\begin{aligned} &x=2 \\ &x=3\\ \end{aligned}\right.\right. $.
Vậy $x \in\{2 ; \, 3\}$.
Câu 8. (2,5 điểm): Thực hiện các phép tính:
a) $\left(6 x^8 y^2-27 x^8 y\right): 3 x y$.
b) $\left(2 x^2+16 x^8+3 x-4\right)$ : $(2 x-1)$.
c) $\dfrac{x^2}{x^2-4}+\dfrac{1}{x-2}+\dfrac{1}{x+2}$.
Hướng dẫn giải:
a) $\left(6 x^3 y^2-27 x^3 y\right): 3 x y=2 x^2 y-9 x^2$
b)
| $-$ | $16 x^3+2 x^2+3 x-4$ | $2 x-1$ | |
| $16 x^3-8 x^2$ | $8 x^2+5 x+4$ | ||
| $-$ | $10 x^2+3 x-4$ | ||
| $10 x^2-5 x$ | |||
| $-$ | $8 x-4$ | ||
| $8 x-4$ | |||
| $0$ |
Vậy $\left(2 x^2+16 x^3+3 x-2\right) \, : \, (2 x-1)=8 x^2+5 x+4$.
c) ĐKXĐ: $x \neq \pm 2$.
$\dfrac{x^2}{x^2-4}+\dfrac{1}{x-2}+\dfrac{1}{x+2}=\dfrac{x^2}{(x-2)(x+2)}+\dfrac{1}{x-2}+\dfrac{1}{x+2}$
$=\dfrac{x^2+x+2+x-2}{(x-2)(x+2)} =\dfrac{x^2+2 x}{(x-2)(x+2)}$
$=\dfrac{x(x+2)}{(x-2)(x+2)}=\dfrac{x}{x-2}$.
Câu 9. (2,5 điểm):
Cho tam giác $A B C$ vuông tại $A,$ $A B<A O$, đường cao $A H$. Kẻ $H D$ vuông góc với $A B$ tại $D$, $H E$ vuông góc với $A C$ tại $E$.
a) Tứ giác $A D H E$ là hình gì? Vì sao?
b) Tính diện tích của tứ giác $A D H E$ nếu $A D=4 $ cm; $A H=5$ cm.
c) Gọi $I$ là điểm đối xứng của $B$ qua $D$, $K$ là điểm đối xứng của $H$ qua $D$. Chứng minh tứ giác $B K I H$ là hình bình hành; $A K$ vuông góc với $I H$.
Hướng dẫn giải:
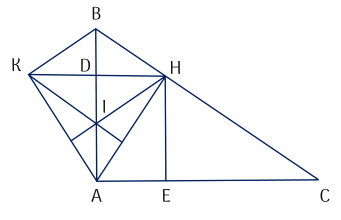
a) $\triangle A B C$ vuông tại $A$ suy ra $\widehat{BAC}=90^{\circ} \Rightarrow \widehat{DAE}=90^{\circ}$.
Do $H D \perp A B \Rightarrow \widehat{H D A}=90^{\circ}$;
$H E \perp A C \Rightarrow \widehat{H E A}=90^{\circ}$.
Tứ giác $A D H E$ có $\widehat{D A E}=\widehat{H D A}=\widehat{H E A}=90^{\circ}$ suy ra tứ giác $A D H E$ là hình chữ nhật.
b) Do $\triangle A H D$ vuông tại $D$, áp dụng định lý Py-ta-go suy ra $A H^2=A D^2+D H^2$
$\Rightarrow 25=16+D H^2 \Rightarrow D H^2=9 \Rightarrow D H=3$ cm.
Do $A D H E$ là hình chữ nhật suy ra $S_{A D H E}=A D . D H=4.3=12$ cm$^2$.
c) Do $I$ là điểm đối xứng với $B$ qua $D$ suy ra $D B=D I$. (1)
Do $K$ là điểm đối xứng với $H$ qua $D$ suy ra $D K=D H$. (2)
Từ (1) và (2) suy ra $B K I H$ là hình bình hành suy ra $K I$ // $B H$
mà $A H \perp B H \Rightarrow K I \perp A H$.
$\Delta A K H$ có $A D \perp K H $; $K I \perp A H$ suy ra $I$ là trực tâm của $\triangle A K H$ suy ra $H I \perp A K$.
Câu 10. (1 điểm):
1. Bác Bình cần lát gạch cho một cái sân hình chữ nhật có chiều dài là $9$ m, chiều rộng bằng $8$ m. Bác chọn các viên gạch hình vuông cạnh $5$ dm để lát lên sân đó. Tính số tiền mà bác Bình phải trả để mua gạch lát đủ sân, biết giá mỗi viên gạch là $35$ $000$ đồng và diện tích phần mạch vữa là không đáng kể.
2. Cho hai số $x$, $y$ thỏa mãn điều kiện $x^2+5 y^2-4 x-4 x y+6 y+5=0$. Tính giá trị của biểu thức $P=(x-3)^{2021}+(y-2)^{2021}+(x+y-5)^{2021}$.
Hướng dẫn giải:
1) Diện tích của cái sân là: $9.8=72$ (m$^2$).
Đổi $5$ dm = $0,5$ m.
Diện tích một viên gạch là: $0,5 . 0,5=0,25$ (m$^2$).
Số viên gạch cần để lát hết sân là: $72: 0,25=288$ (viên).
Số tiền bác Bình phải trả để mua gạch lát sân là: $288.35 \, 000=10 \, 080 \, 000$ (đồng).
Vậy bác Bình phải trả $10 \, 080 \, 000$ đồng.
2) Ta có $x^2+5 y^2-4 x-4 x y+6 y+5=0$
$\Leftrightarrow x^2-2 x(2+2 y)+5 y^2+6 y+5=0$
$\Leftrightarrow x^2-2 x(2+2 y)+\left(4 y^2+8 y+4\right)+\left(y^2-2 y+1\right)=0$
$\Leftrightarrow\left[x^2-2 x(2+2 y)+(2 y+2)^2\right]+(y-1)^2=0$
$\Leftrightarrow(x-2 y-2)^2+(y-1)^2=0$ (1).
Mà $(x-2 y-2)^2 \geq 0$; $(y-1)^2 \geq 0$ nên (1) xảy ra khi $\left\{\begin{aligned}&x-2 y-2=0 \\ &y-1=0\\ \end{aligned} \Leftrightarrow\left\{\begin{aligned}&x=4 \\& y=1\\ \end{aligned}\right.\right.$
Thay $\left\{\begin{aligned}&x=4 \\ &y=1\\ \end{aligned}\right.$ vào $P=(x-3)^{2021}+(y-2)^{20212}+(x+y-5)^{2021}$ ta được;
$P=(4-3)^{2021}+(1-2)^{20021}+(4+1-5)^{20212}=1-1+0=0$.
Vậy $P=0$.
