Con lắc lò xo SVIP

I. Con lắc lò xo

Con lắc lò xo là một hệ bao gồm một vật nặng có khối lượng \(m\) được gắn với một lò xo có độ cứng \(k\) và có khối lượng không đáng kể.

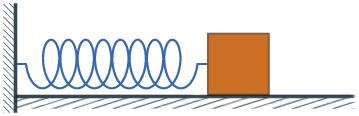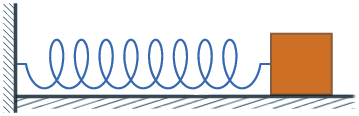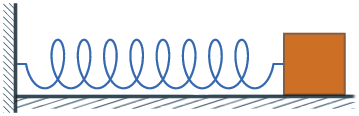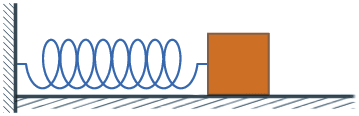
Đối với con lắc lò xo nằm ngang, vị trí cân bằng là vị trí mà lò xo không biến dạng.

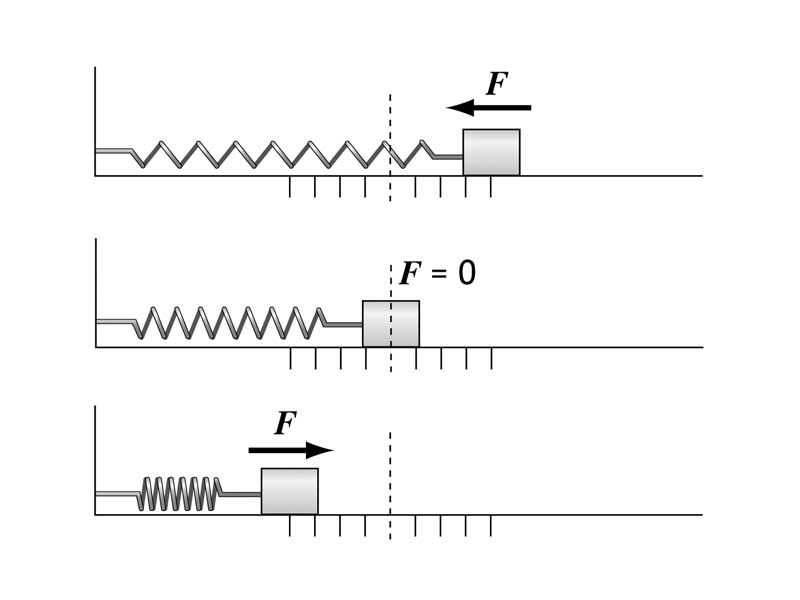
Khi kéo vật ra khỏi vị trí cân bằng để lò xo dãn ra một đoạn rồi buông tay, thấy vật dao động trên một đoạn thẳng quanh vị trí cân bằng.

Dao động của của vật có phải là dao động điều hòa không?

II. Khảo sát dao động của con lắc lò xo về mặt động lực học

1. Xét một con lắc lò xo nằm ngang

Ở vị trí vật có li độ \(x\) thì lò xo biến dạng một đoạn \(\Delta l=x\).

Khi đó lực đàn hồi là \(F=-kx\)

Áp dụng định luật II Newton ta có

\(F=ma\)

\(\Rightarrow-kx=ma\)

\(\Rightarrow a=-\dfrac{k}{m}x\)

Đặt \(\omega^2=\dfrac{k}{m}\Rightarrow a=-\omega^2x\)

Vậy dao động của con lắc lò xo là dao động điều hòa với tần số góc:

\(\omega=\sqrt{\dfrac{k}{m}}\)

2. Lực kéo về

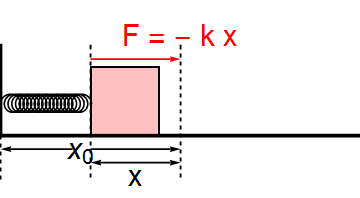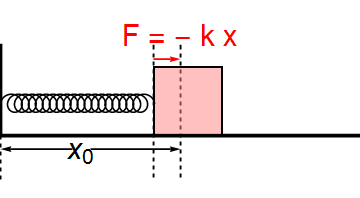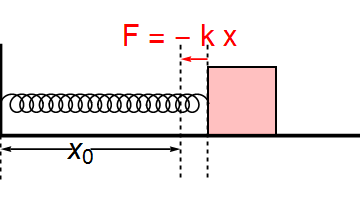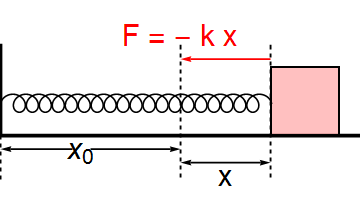
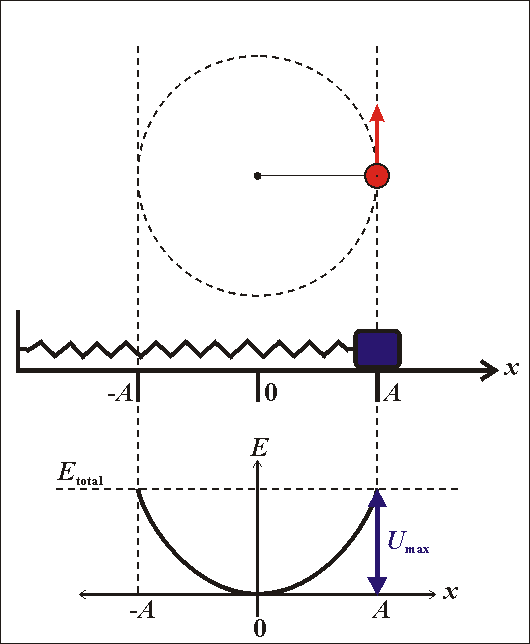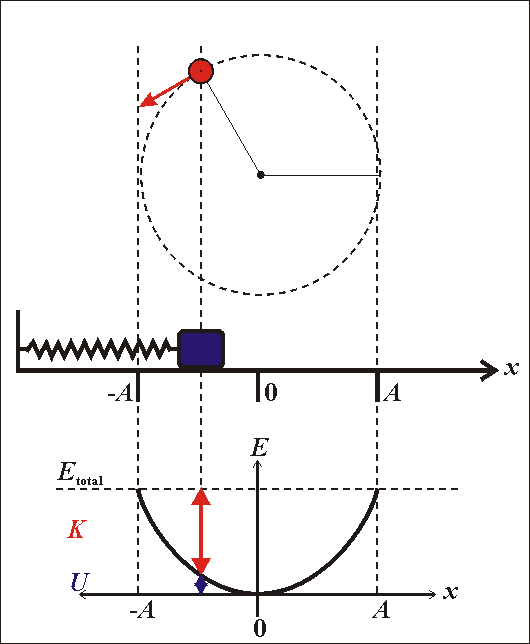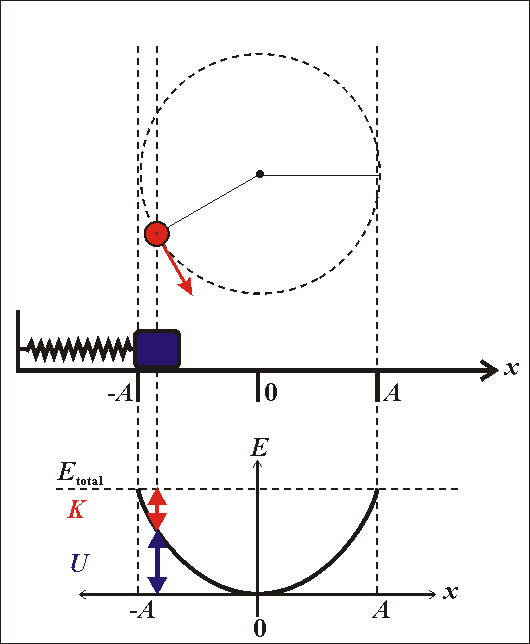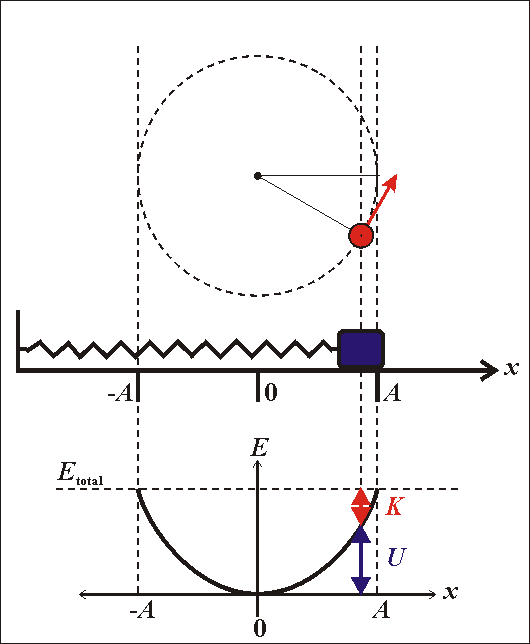
• Động năng của con lắc lò xo

\(W_đ=\dfrac{1}{2}mv^2\)

• Thế năng của con lắc lò xo

\(W_t=\dfrac{1}{2}kx^2\)

• Cơ năng của con lắc lò xo

\(W=W_đ+W_t\)

\(\Rightarrow W=\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2\)

\(\Rightarrow W=\dfrac{1}{2}m\omega^2A^2\sin^2\left(\omega t+\varphi\right)+\dfrac{1}{2}mA^2\cos^2\left(\omega t+\varphi\right)\)

Vậy

\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}kA^2=const\)

Nhận xét: 

• Cơ năng của con lắc tỉ lệ với bình phương biên độ dao động
• Cơ năng của con lắc được bảo toàn nếu bỏ qua mọi ma sát
• Trong quá trình dao động của con lắc, động năng và thế năng chuyển hóa lẫn nhau