Chứng minh một đường thẳng là tiếp tuyến của đường tròn SVIP

Hướng dẫn giải:

kéo dài CI cắt AD tại E.

Chứng minh được CI = IE nên tam giác CDE cân tại D.

Suy ra DI là phân giác góc D, khi đó IH = IA. Vậy DC là tiếp tuyến của đường tròn đường kính AB.

Hướng dẫn giải:

Kẻ OI $\bot$ AB ( I $\in$ CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.

Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.

Ta có \(IO=\dfrac{CA+DB}{2}=\dfrac{MC+MD}{2}=\dfrac{DC}{2}\) là bán kính của đường tròn (I).

Do đó AB tiếp xúc với đường tròn đường kính CD.

Hướng dẫn giải:

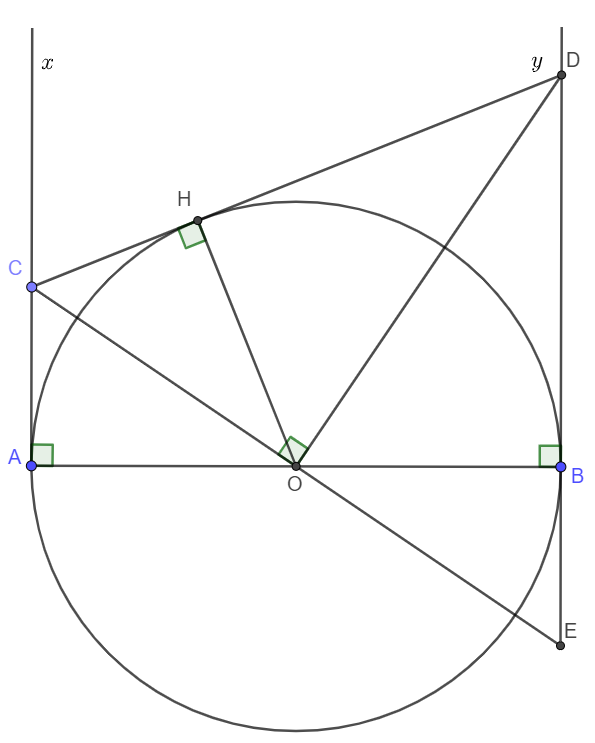
Vẽ \(OH\perp CD\left(H\in CD\right)\). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \(\Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OE\).
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
\(OH\perp DC,OB\perp DE\Rightarrow OH=OB.\).
Suy ra CD tiếp xúc với (O) tại H.
Ta có \(OH\perp CD,OH=OB=r\).
Vậy CD là tiếp tuyến của đường tròn (O).

Hướng dẫn giải:

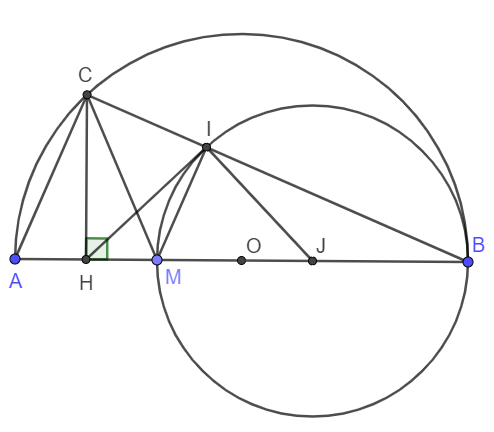
Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên \(\widehat{MIB}=90^o\Rightarrow\widehat{CIM}=90^o\).

Vậy nên tứ giác CHMI nội tiếp.

\(\Rightarrow\widehat{HIM}=\widehat{HCM}\).

Tam giác ACM cân tại C nên \(\widehat{HCM}=\widehat{HCA}\).

Mà \(\widehat{HCA}=\widehat{HBC}\) (Cùng phụ góc CAB)

Tam giác IJB cân tại J nên \(\widehat{HBC}=\widehat{JIB}\).

Tóm lại : \(\widehat{HIM}=\widehat{JIB}\Rightarrow\widehat{HIM}+\widehat{MIJ}=\widehat{JIB}+\widehat{MIJ}\)

\(\Rightarrow\widehat{HIJ}=\widehat{MIB}=90^o.\)

Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB.

Hướng dẫn giải:

Do \(\widehat{AEH}=\widehat{ADH}=90^o\) nên tứ giác AEHD nội tiếp đường tròn.
Suy ra đường tròn ngoại tiếp tam giác AED chính là đường tròn đường kính AH.

Do H là giao điểm hai đường cao BD và CE nên H là trực tâm. Thế thì AH \(\perp\) BC.
Suy ra  \(\widehat{DAH}=\widehat{DBC}\) (vì cùng phụ với góc \(\widehat{DCB}\)).
Tam giác BDC vuông tại D có I là trung điểm của BC nên IB = ID = IC.
Suy ra tam giác IBD cân ở I.  Vì vậy \(\widehat{IDB}=\widehat{DBI}\).
Từ đó suy ra: \(\widehat{HAD}=\widehat{HBI}=\widehat{BDI}\)  hay  \(\widehat{HAD}=\widehat{HDI}\).

Gọi J là trung điểm AH. Ta có \(\widehat{HAD}=\widehat{JDA}\Rightarrow\widehat{JDA}=\widehat{HDI}\).

Vậy nên \(\widehat{JDI}=\widehat{HDI}+\widehat{JDH}=\widehat{JDA}+\widehat{FDH}=\widehat{ADH}=90^o\).
Suy ra DI là tiếp tuyến của đường tròn đường kính AH.
Chứng minh tương tự ta cũng có EI là tiếp tuyến của đường kính AH.

Hướng dẫn giải:

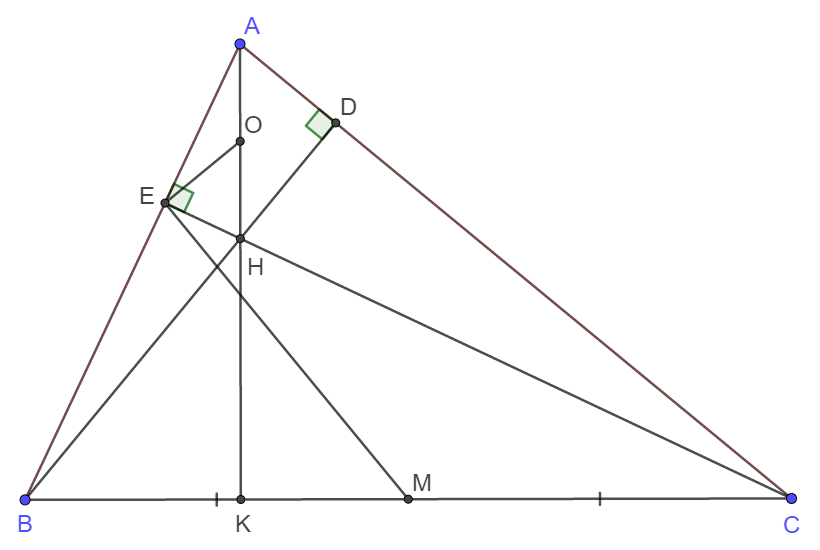
a) Ta thấy tam giác AEH và ADH đều là các tam giác vuông chung cạnh huyền AH nên AEHD nội tiếp đường tròn đường kính AH.
b)  Gọi O là trung điểm của AH và K là giao điểm của AH với BC. Do H là trực tâm nên ta có ngay AK là đường cao của tam giác ABC.

Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta có:
\(\widehat{OEH}=\widehat{OHE}=\widehat{KHC}\); \(\widehat{MEC}=\widehat{MCE}\).
mà \(\widehat{KHC}+\widehat{MCE}=90^o\).
Suy ra: \(\widehat{OEH}+\widehat{MEC}=90^o\) nên \(OE\perp EM\) hay ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHD.

Hướng dẫn giải:

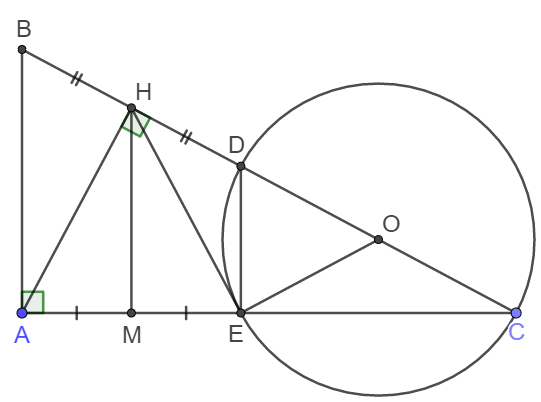
a) Gọi O là trung điểm của CD.

Do E nằm trên đường tròn (O) nên \(\widehat{DEC}=90^o\) hay \(DE\perp AC\).

Thế thì DE//AB.

Gọi M là trung điểm AE, xét hình thang ABDE có: H là trung điểm BD và M là trung điểm AE nên HM là đường trung bình của hình thang.

Vậy nên HM//AB//DE hay \(HM\perp AE.\)

Suy ra tam giác HAE cân tại H hay \(\widehat{HEA}=\widehat{HAE}\).

Tam giác OEC cân tại O nên \(\widehat{OEC}=\widehat{OCE}\).

Từ đó ta có: \(\widehat{HEA}+\widehat{OEC}=\widehat{HAE}+\widehat{OCE}=90^o.\)

Suy ra \(\widehat{OEH}=180^o-90^o=90^o.\)
Vậy nên $HE$ là tiếp tuyến của đường tròn (O).
b) Xét tam giác ABC vuông tại A, áp dụng định lý Pi-ta-go, ta có:

\(BC=\sqrt{AB^2+AC^2}=17\left(cm\right)\)

Do tam giác HAE cân tại H nên:

HE = AH = \(\dfrac{AB.AC}{BC}=\dfrac{120}{17}.\)