Chứng minh hình học liên quan tới góc nội tiếp SVIP

Hướng dẫn giải:

Kẻ đường kính $AE$ của đường tròn $(O)$.

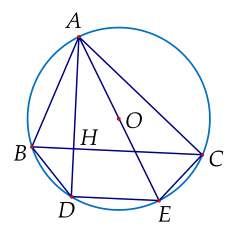
Ta thấy $\widehat{ACE}=90^\circ$ (góc nội tiếp chắn nửa đường tròn).

Từ đó $\widehat{OAC}+\widehat{AEC}=90^\circ$ (1).

Theo giả thiết, ta có:

$\widehat{BAH}+\widehat{ABC}=90^\circ$ (2).

Mà $\widehat{AEC}=\widehat{ABC}$ (cùng chắn $\overset\frown{AC}$) (3).

Từ (1),(2) và (3) suy ra $\widehat{BAH}=\widehat{OAC}$ (đpcm).

Hướng dẫn giải:

Vẽ đường kính $AD$ của đường tròn $(O)$, suy ra $\widehat{ACD}=90^\circ$ (góc nội tiếp chắn nửa đường tròn).

Xét $\Delta HBA$ và $\Delta CDA$ có:

$\widehat{AHB}=\widehat{ACD} = 90^\circ$;

$\widehat{HBA}=\widehat{CDA}$ (góc nội tiếp cùng chắn $\overset\frown{AC}$);

Do đó $\Delta HBA \backsim \Delta CDA$

Suy ra $\dfrac{AH}{AC}=\dfrac{AB}{AD}$ nên $AB.AC=AD.AH$.

Mà $AD=2R$.

Do đó $AB.AC=2R.AH$.

Hướng dẫn giải:

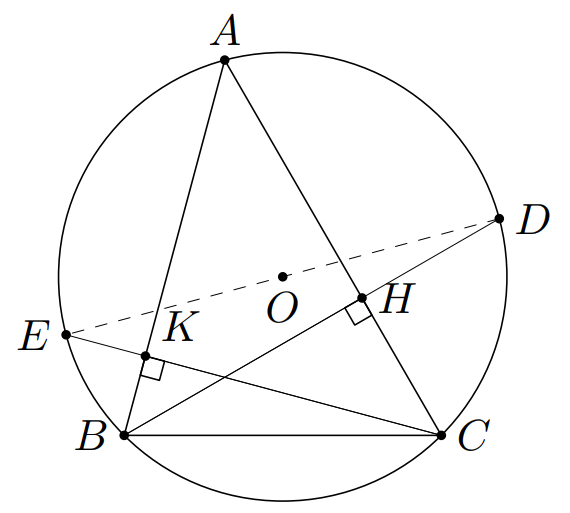
Ta có $BH \perp AC$ nên $\Delta ABH$ vuông tại $H$.

Mà $\widehat{BAH}= 45^\circ$ nên $\widehat{ABH'} = 45^\circ$.

Mặt khác $\widehat{ABD} = \widehat{ACD}$ (góc nội tiếp cùng chắn cung $AD$) nên $\widehat{ACD} = 45^\circ$. (1)

$CK \perp AB$ nên $\Delta ACK$ vuông tại $K$.

Mà $\widehat{CAK} = 45^\circ$ nên $\widehat{ACK} = 45^\circ$. (2)

Từ (1) và (2) ta có $\widehat{DCE} = 90^\circ$ nên $DE$ là đường kính.

Vậy $D$, $O$, $E$ thẳng hàng.