Bất phương trình bậc nhất hai ẩn SVIP

I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bất phương trình bậc nhất hai ẩn \(x,y\) là bất phương trình có một trong các dạng sau:

\(ax+by< c;ax+by>c;ax+by\le c;ax+by\ge c.\)

trong đó \(a,b,c\) là những số thực đã cho với \(a,b\)  không đồng thời bằng \(0\) , \(x\) và \(y\) là các ẩn.

Ví dụ. \(3x-2y< 4\)  và \(x+6y\ge\dfrac{-1}{3}\) là những bất phương trình bậc nhất hai ẩn. 

Cho bất phương trình bậc nhất hai ẩn \(ax+by< c\) (*).

Mỗi cặp số \(\left(x_0;y_0\right)\) sao cho \(ax_0+by_0< c\) được gọi là một nghiệm của bất phương trình (*).

Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm có tọa độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.

Chú ý: Nghiệm và miền nghiệm của các bất phương trình dạng \(ax+by>c,ax+by\le c,ax+by\ge c\) được định nghĩa tương tự.

Ví dụ. Cho bất phương trình bậc nhất hai ẩn \(2x+y< 6\). Cặp số nào sau đây là một nghiệm của bất phương trình trên?

a) \(\left(x;y\right)=\left(1;2\right)\);              b) \(\left(x;y\right)=\left(4;-1\right)\).

Giải

a) Vì \(2.1+2=4< 6\) nên cặp số \(\left(1;2\right)\) là một nghiệm của bất phương trình đã cho.

b) Vì \(2.4+\left(-1\right)=7>6\) nên cặp số \(\left(4;-1\right)\) không phải là một nghiệm của bất phương trình đã cho.

II. BIỂU DIỄN MIỀN NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.

 1. Mô tả miền nghiệm của bất phương trình bậc nhất hai ẩn

Trong mặt phẳng tọa độ \(Oxy\), phương trình \(ax+by=c\) (với \(a,b\) không đồng thời bằng \(0\)) xác định một đường thẳng \(d\) như sau:

• \(d\) có phương trình là \(x=\dfrac{c}{a}\) nếu \(b=0\);
• d có phương trình là \(y=-\dfrac{a}{b}x+\dfrac{c}{b}\) nếu \(b\ne0\). 

Trong mặt phẳng tọa độ \(Oxy\) đường thẳng \(d:ax+by=c\) chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể \(d\)) là miền nghiệm của bất phương trình \(ax+by< c\), nửa mặt phẳng còn lại (không kể \(d\)) là miền nghiệm của bất phương trình \(ax+by>c.\)

Chú ý: Bất phương trình dạng \(ax+by\le c\) hoặc \(ax+by\ge c\) thì miền nghiệm là nửa mặt phẳng kể cả đường thẳng \(d\).

2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn.

Các bước biểu diễn miền nghiệm của bất phương trình \(ax+by< c\) trong mặt phẳng tọa độ \(Oxy:\)

Bước 1. Vẽ đường thẳng \(d:ax+by=c\). Đường thẳng \(d\) chia mặt phẳng tọa độ thành hai nửa mặt phẳng.

Bước 2. Lấy một điểm \(M\left(x_0;y_0\right)\) không nằm trên \(d\) (ta thường lấy gốc tọa độ \(O\) nếu \(c\ne0\)). Tính \(ax_0+by_0\) và so sánh với \(c.\)

Bước 3. Kết luận

• Nếu \(ax_0+by_0< c\) thì nửa mặt phẳng (không kể \(d\)) chứa điểm \(M\) là miền nghiệm của bất phương trình \(ax+by< c\)
• Nếu \(ax_0+by_0>c\)  thì nửa mặt phẳng (không kể \(d\)) không chứa điểm \(M\) là miền nghiệm của bất phương trình \(ax+by< c\)

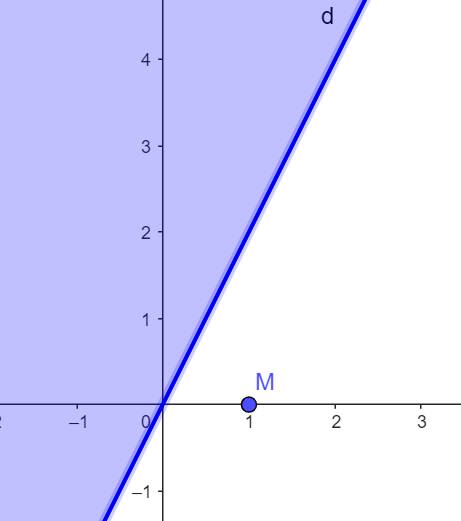
Ví dụ. Biểu diễn miền nghiệm của bất phương trình \(2x-y\ge0\) trên mặt phẳng tọa độ?

Giải.

Ta biểu diễn miền nghiệm của bất phương trình \(2x-y\ge0\) trên mặt phẳng tọa độ như sau:

Vẽ đường thẳng \(d:2x-y=0\) trên mặt phẳng tọa độ.

Lấy điểm \(M\left(1;0\right)\)  không thuộc \(d\) . Ta có \(2.1-0=2>0\) do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ \(d\) chứa điểm \(M\)(miền không tô màu) trong hình vẽ sau