Bài tập mẫu: Thiết diện SVIP

Hướng dẫn giải:

Trong (SBC): MN $\cap $ BC = E

Vậy (ABCD) $\cap$ (AMN) = AE

Trong (ABCD): AE $\cap $ CD = K

Vậy thiết diện cần tìm là tứ giác MNKA.

Hướng dẫn giải:

Do O \(\in\) (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.

Trong (SDC) : MN \(\cap\) CD = K

Trong (ABCD):

    KO \(\cap\) AC = P

    KO \(\cap\) BD = Q

Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.

Chú ý: Thiết diện là phần chung của hình chóp với mặt phẳng (OMN), nên do đó ta không cần tìm giao tuyến giữa (OMN) và (SAB) do giao tuyến đó nằm hoàn toàn bên ngoài hình chóp (các bạn tự tưởng tưởng hoặc dựng thêm cũng được). 

Hướng dẫn giải:

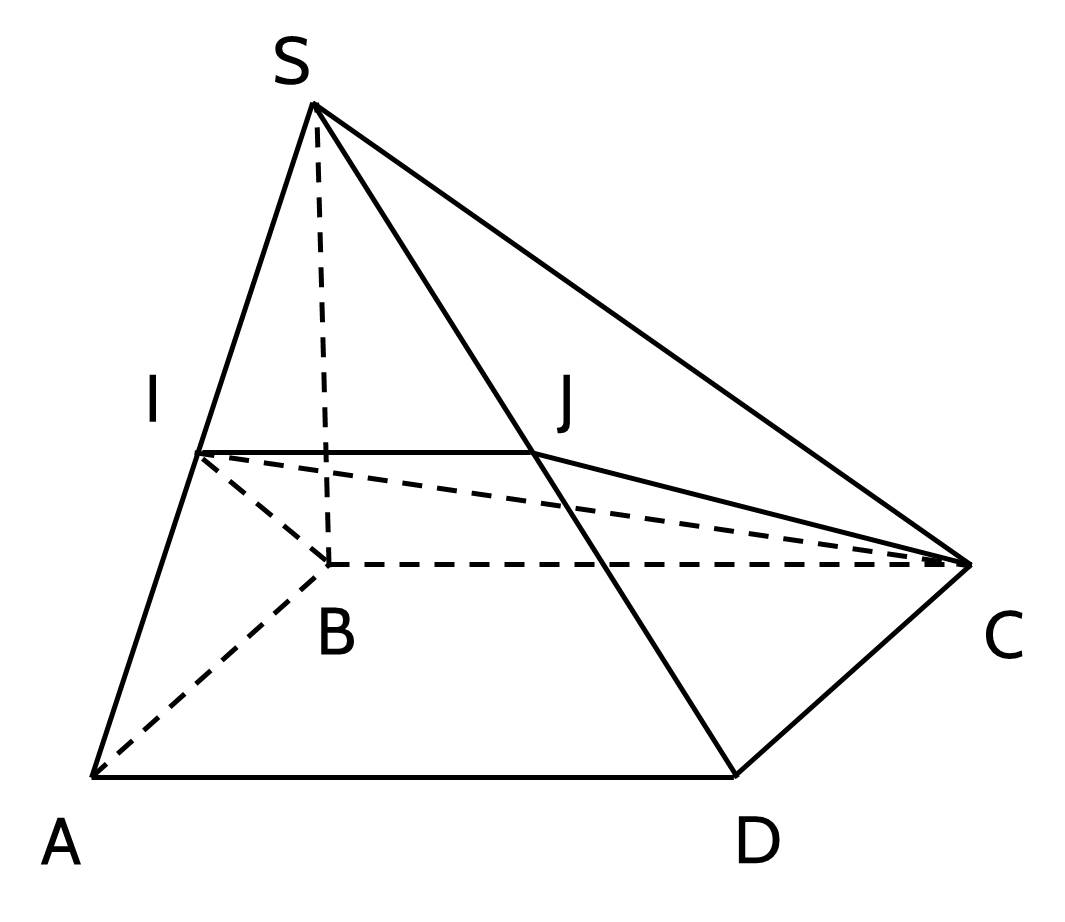
Gọi $O$ là giao điểm của $A C$ và $B D, G$ là giao điểm của $C I$ và $S O$.

Khi đó $G$ là trọng tâm tam giác $\mathrm{S} A C$. Suy ra $G$ là trọng tâm tam giác $S B D$.

Gọi $J=B G \cap S D$. Khi đó $J$ là trung điểm $S D$.

Do đó thiết điện của hình chóp cắt bởi $(I B C)$ là hình thang $I J C B$ ( $J$ là trung điểm $S D$ ).