Ta có: \(\dfrac{a}{c}\) = \(\dfrac{c}{b}\)

⇔ c2 = ab

Ta lại có: \(\dfrac{a^2+c^2}{b^2+c^2}\) = \(\dfrac{a^2+ab}{b^2+ab}\)

                                        = \(\dfrac{a.\left(a+b\right)}{b.\left(a+b\right)}\)

                                        = \(\dfrac{a}{b}\)

a) Vẽ hình

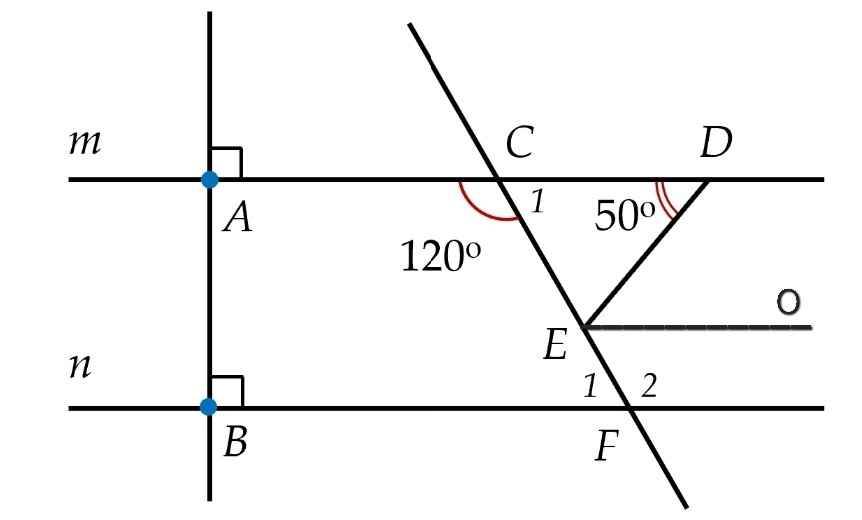 b) Ta có:

∠C₁ + ∠ACF = 180⁰ (kề bù)

⇒ ∠C₁ = 180⁰ - ∠ACF

= 180⁰ - 120⁰

= 60⁰

Do m // n (gt)

⇒ ∠F₁ = ∠C₁ = 60⁰ (so le trong)

c) Do AB ⊥ m (gt)

m // n (gt)

⇒ AB ⊥ n

d) Vẽ tia Eo // m // n như hình

Do Eo // m

⇒ ∠DEo = ∠ADE = 50⁰ (so le trong)

Do Eo // n

⇒ ∠FEo = ∠F = 60⁰ (so le trong)

⇒ ∠DEF = ∠DEo + ∠FEo

= 50⁰ + 60⁰

= 110⁰

Gọi a (quyển), b (quyển), c (quyển) lần lượt là số quyển sách ba lớp 7A, 7B, 7C đã quyên góp (a, b, c ∈ ℕ*)

Do tổng số quyển sách đã quyên góp là 180 quyển nên:

a + b + c = 180

Do số quyển sách của ba lớp 7A, 7B, 7C tỉ lệ với các số 5; 6; 4 nên:

\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{4}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{4}\) = \(\dfrac{a+b+c}{5+6+4}\) = \(\dfrac{180}{15}\) = 12

\(\dfrac{a}{5}\) = 12 ⇒ a = 12.5 = 60

\(\dfrac{b}{6}\) = 12 ⇒ b = 12.6 = 72

\(\dfrac{c}{4}\) = 12 ⇒ c = 12.4 = 48

Vậy số quyển sách đã quyên góp của lớp 7A, 7B, 7C lần lượt là: 60 quyển, 72 quyển, 48 quyển

a) \(\dfrac{1}{12}\)

b) TH1: \(\dfrac{-1}{15}\); TH2: \(\dfrac{11}{15}\)

c) 10

a) 7/2 - (3/4 + 1/5)

= 7/2 - 19/20

= 51/20

b) 12/23 . 7/13 + 11/23 . 7/13

= 7/13 . (12/23 + 11/23)

= 7/13 . 1

= 7/13

c) |-2| - (5/9 - 2/3)² : 4/27

= 2 - 1/81 : 4/27

= 2 - 1/12

= 23/12

GT

KL

GT

KL

a) Bằng nhau

b) Cắt

a) Bằng nhau

b) Cả hai đường thẳng vuông góc với đt thứ 3

Giả thiết: Một đường thẳng vuông góc với một trong hai đường thẳng song song.

Kết luận: Nó cũng vuông góc với đường thẳng còn lại.