

Vũ Phương Anh
Giới thiệu về bản thân



































a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
COE
(hai góc tương ứng)
là tia phân giác của .
Cho , , là tia phân giác . Trên tia lấy điểm bất kì. Gọi lần lượt là chân đường vuông góc kẻ từ đến và . Chứng minh:
a) .
b) .
Hướng dẫn giải: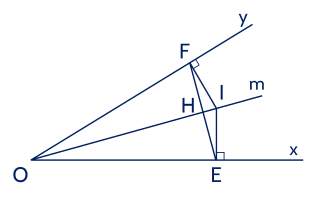
a) Xét và có
(giả thiết);
cạnh chung;
( là tia phân giác).
Vậy (cạnh huyền - góc nhọn).
b) (chứng minh trên)
(hai cạnh tương ứng).
Gọi là giao điểm của và .
Xét và , có
(chứng minh trên);
( là tia phân giác);
chung.
Do đó (c.g.c)
(hai góc tương ứng)
Mà nên .
Vậy .
Ta có thuộc phân giác của ;
; (tính chất tia phân giác của một góc).
Gọi là trung điểm của .
Xét và , có
( là trung trực của ),
(già thiết),
là cạnh chung.
Do đó (hai cạnh góc vuông)
(hai cạnh tương ứng).
Xét và , có
(giả thiết);
(chứng minh trên);
(chứng minh trên).
Do đó (cạnh huyền - cạnh góc vuông)
(hai cạnh tương ứng).