

Tường Bùi
Giới thiệu về bản thân



































Hướng dẫn giải:
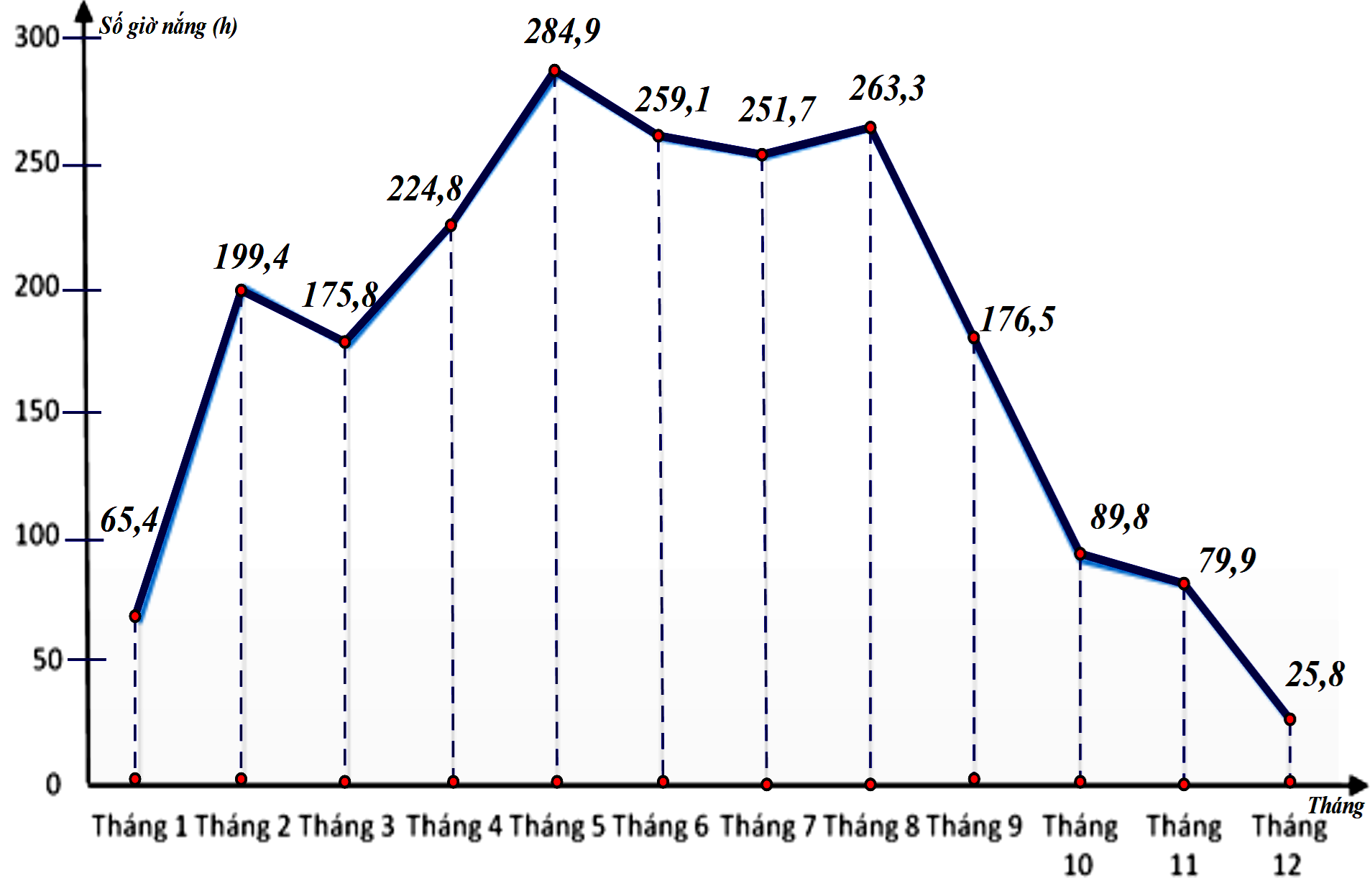
Hướng dẫn giải:

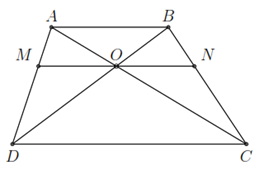
Xét ΔADCΔADC có MOMO // DCDC nên theo định lí Thalès ta có
OMDC=OAACDCOM=ACOA. (1)
Xét ΔBCDΔBCD có ONON // CDCD nên theo định lí Thalès ta có
ONCD=BNBCCDON=BCBN. (2)
Xét Δ CABΔ CAB có ONON // CDCD nên theo định lí Thalès ta có
BNBC=AOACBCBN=ACAO. (3)
Từ (1)(1), (2)(2), (3)(3) suy ra OMDC=OAAC=BNBC=ONCDDCOM=ACOA=BCBN=CDON.
Suy ra OM=ONOM=ON.
Đổi đơn vị: 1,51,5 m =150=150 cm.
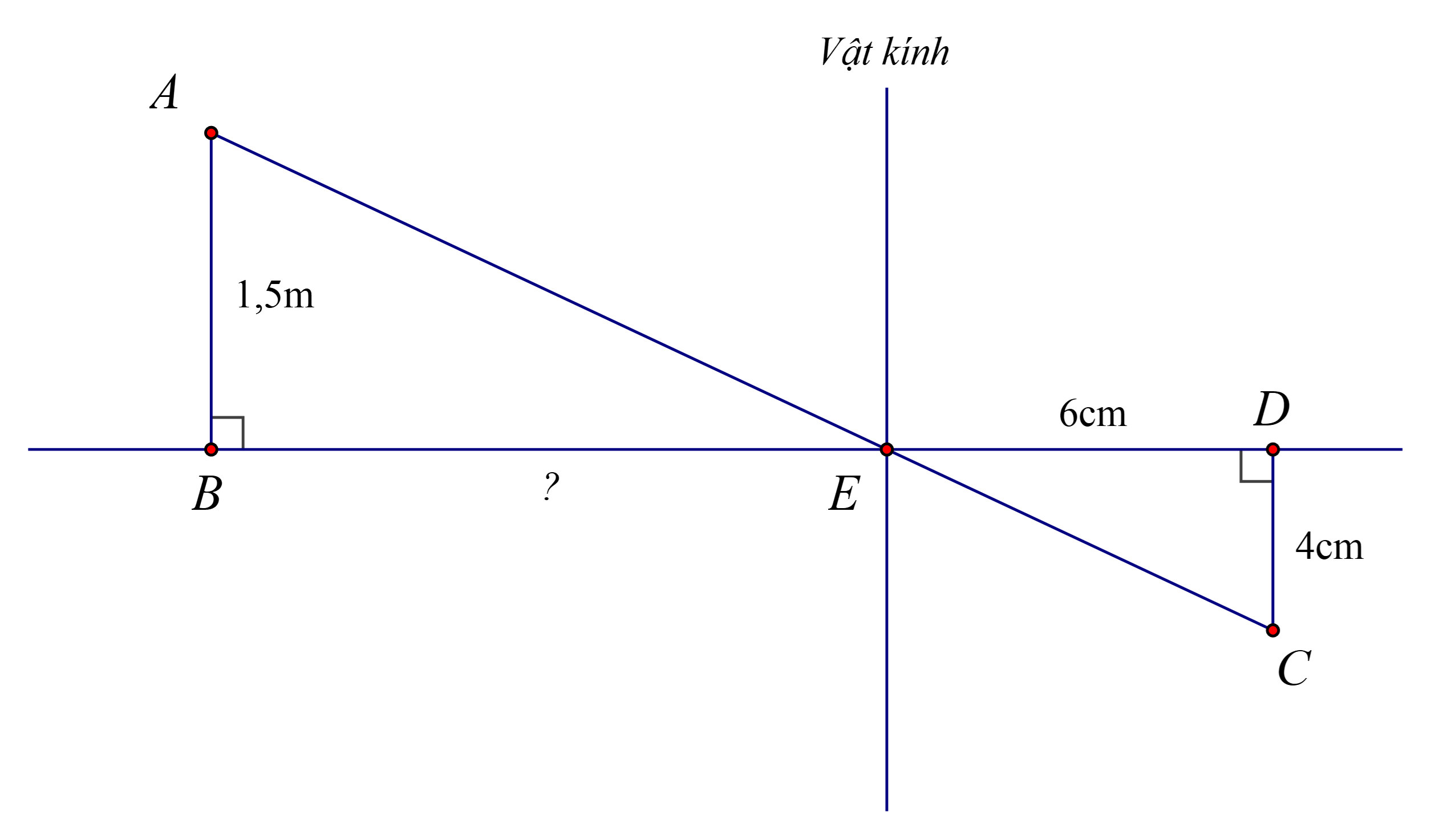
Ta có ABAB // CDCD (cùng vuông góc BDBD) suy ra EBED=ABDCEDEB=DCAB (định lí Thalès)
Suy ra EB=AB.EDDC=150.64=225EB=DCAB.ED=4150.6=225 (cm).
Vậy người đứng cách vật kính máy ảnh là 225225 cm.
a) Ta có:
𝑥
−
3
=
(
3
−
𝑥
)
2
x−3=(3−x)
2
(
𝑥
−
3
)
−
(
𝑥
−
3
)
2
=
0
(x−3)−(x−3)
2
=0
(
𝑥
−
3
)
(
4
−
𝑥
)
=
0
(x−3)(4−x)=0
𝑥
∈
{
3
;
4
}
x∈{3;4}.
b) Ta có:
𝑥
3
+
3
2
𝑥
2
+
3
4
𝑥
+
1
8
=
1
64
x
3
+
2
3
x
2
+
4
3
x+
8
1
=
64
1
(
𝑥
+
1
2
)
3
=
(
1
4
)
3
(x+
2
1
)
3
=(
4
1
)
3
𝑥
+
1
2
=
1
4
x+
2
1
=
4
1
𝑥
=
−
1
4
x=
4
−1
.
a)
𝑥
2
+
2
𝑥
𝑦
+
𝑦
2
−
𝑥
−
𝑦
=
(
𝑥
+
𝑦
)
(
𝑥
+
𝑦
−
1
)
x
2
+2xy+y
2
−x−y=(x+y)(x+y−1);
b)
2
𝑥
3
+
6
𝑥
2
+
12
𝑥
+
8
=
(
2
𝑥
+
2
)
(
𝑥
2
+
2
𝑥
+
4
)
2x
3
+6x
2
+12x+8= (2x+2)(x
2
+2x+4).