

Đoàn Nguyễn Hoàng Uyên
Giới thiệu về bản thân



































Minh có số quả trứng là:
36 + 69 =105 (quả)
Đáp số: 105 quả trứng
Câu C nha
Để tính các góc của tam giác ABC, ta sử dụng tính chất của tam giác nội tiếp trong đường tròn. Giả sử bán kính đường tròn là R.
Vì AC là dây cung bằng bán kính R, nên AC = OA = OC = R. Do đó, tam giác OAC là tam giác đều, suy ra góc OAC = góc OCA = 60°.
Góc ABC sẽ bằng góc AOC, mà AOC thuộc vào đường tròn, nên theo quy tắc nội tiếp trong đường tròn:
Góc ABC = 12 góc AOC; Góc ABC = 21 góc AOC
Nếu O là tâm và AB là đường kính, thì góc AOC = 180°.
Kết luận:
Góc OAC = 60°
Góc OCA = 60°
Góc ABC = 90° (do là góc vuông).
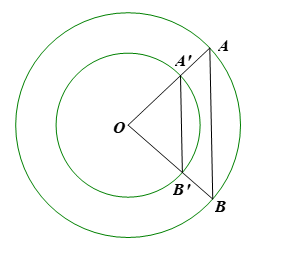
a) Ta có: suy ra
b) Xét ∆OAB có nên AB // A’B’ (theo định lí Thalès đảo).
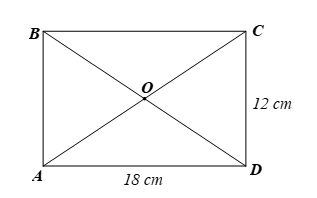
Vì ABCD là hình chữ nhật nên AC = BD. (1)
Gọi O là giao điểm của hai đường chéo AC, BD của hình chữ nhật.
Khi đó, O là trung điểm của AC và BD (tính chất hình chữ nhật) nên (2)
Từ (1) và (2) ta có
Vậy bốn điểm A, B, C, D cùng thuộc một đường tròn đường kính AC, BD.
⦁ Vì ABCD là hình chữ nhật nên
Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:
AC2 = AD2 + DC2 = 182 + 122 = 468.
Do đó
Vậy bán kính đường tròn đi qua bốn điểm A, B, C, D là
a) Vì hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D nên C, D cùng nằm trên hai đường tròn (A; 6 cm) và (B; 4 cm), do đó AC = AD = 6 cm và BC = BD = 4 cm.
b) Do I là giao điểm của đường tròn (B; 4 cm) với đoạn thẳng AB nên I nằm giữa hai điểm A, B và I nằm trên đường tròn (B; 4 cm), do đó BI = 4 cm.
Vì I nằm giữa hai điểm A, B nên ta có: AI + IB = AB
Suy ra AI = AB – IB = 8 – 4 = 4 (cm).
Ta có I nằm giữa hai điểm A, B và AI = BI nên I là trung điểm của đoạn thẳng AB.
c) Do K là giao điểm của đường tròn (A; 6 cm) với đoạn thẳng AB nên K nằm trên đường tròn (A; 6 cm), do đó AK = 6 cm.
Ta có AI < AK (4 cm < 6 cm) nên I nằm giữa hai điểm A, K.
Do đó AI + IK = AK
Suy ra IK = AK – AI = 6 – 4 = 2 (cm).
Vậy IK = 2 cm.

a.Gọi
đối xứng qua
đối xứng với qua
b.Kẻ
đối xứng với qua
a/ BC cố định => B cố định
AB=4 cm không đổi
=> A chạy trên đường tròn tâm B bán kính AB
b/ Từ M dựng đường thẳng // AB cắt BC tại D
=> D là trung điểm của BC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lại)
=> MD là đường trung bình của tg ABC => MD=AB2
Ta có BC cố định =>D cố định
MD không đổi
=> M chạy trên đường tròn tâm D bán kính MD

b: Vì CO=CA(=2cm)
nên O,A cùng nằm trên (C;2cm)
a: Ta có: OA=OB
=>O nằm trên đường trung trực của AB (1)
Ta có: MA=MB
=>M nằm trên đường trung trực của AB (2)
Từ (1),(2) suy ra OM là đường trung trực của AB
b: M là trung điểm của AB
⇒ MA = MB =AB/2 = 8/2 = 4 (cm)
ΔOMA vuông tại M
⇒OM2 + MA2 = OA2
⇔ OM2 = 52 - 42 = 9
⇒ OM = 3 (cm)