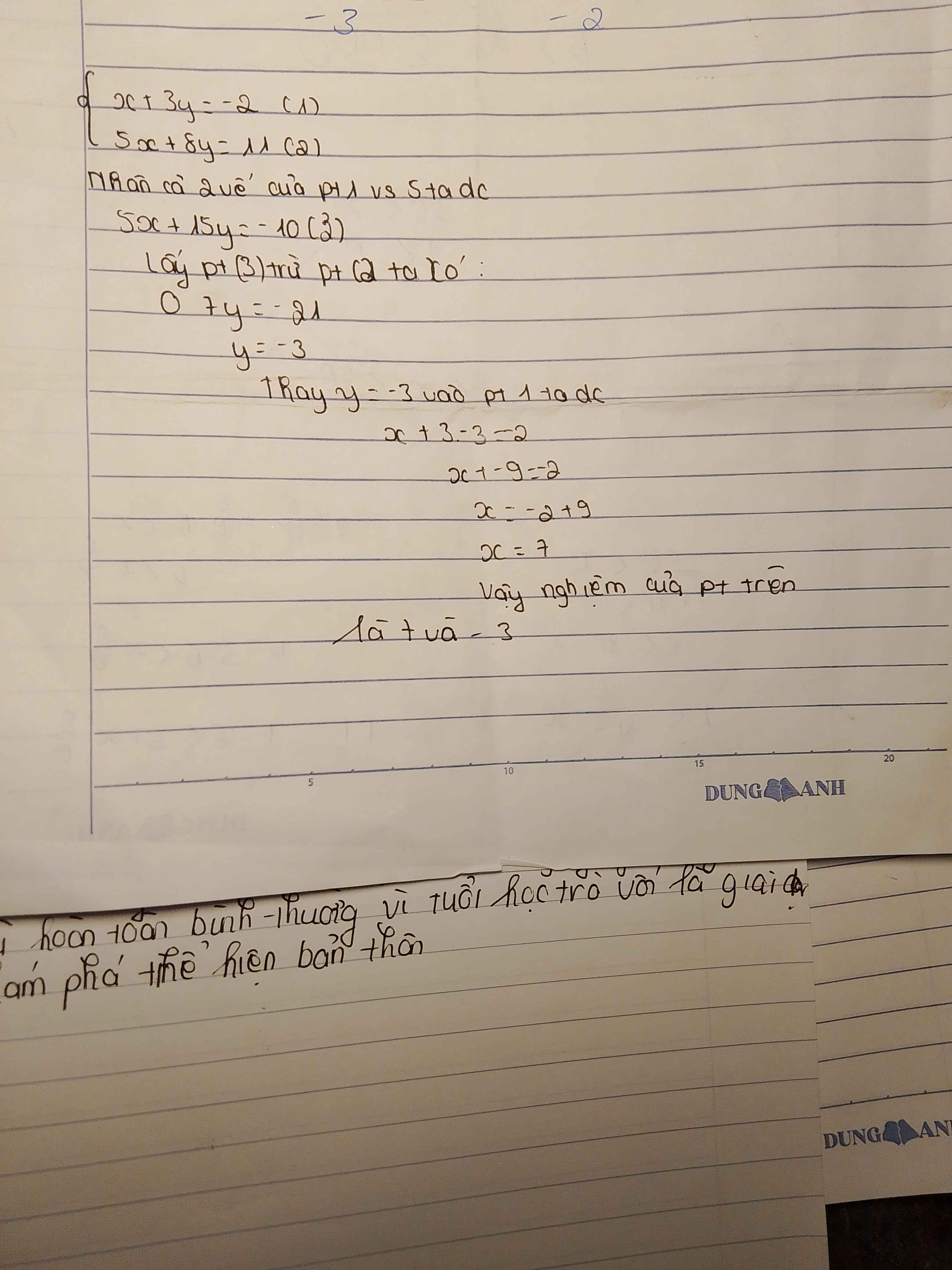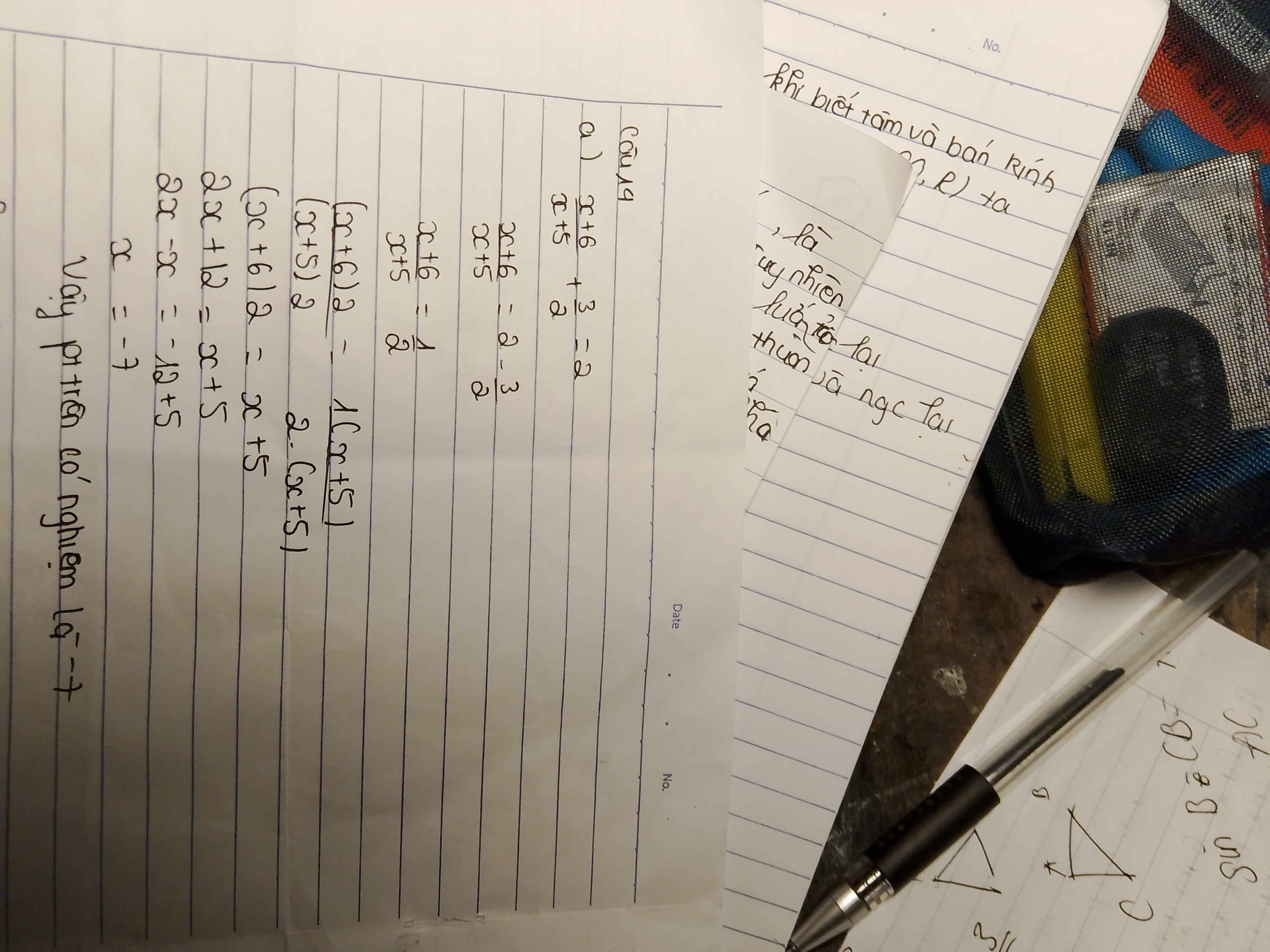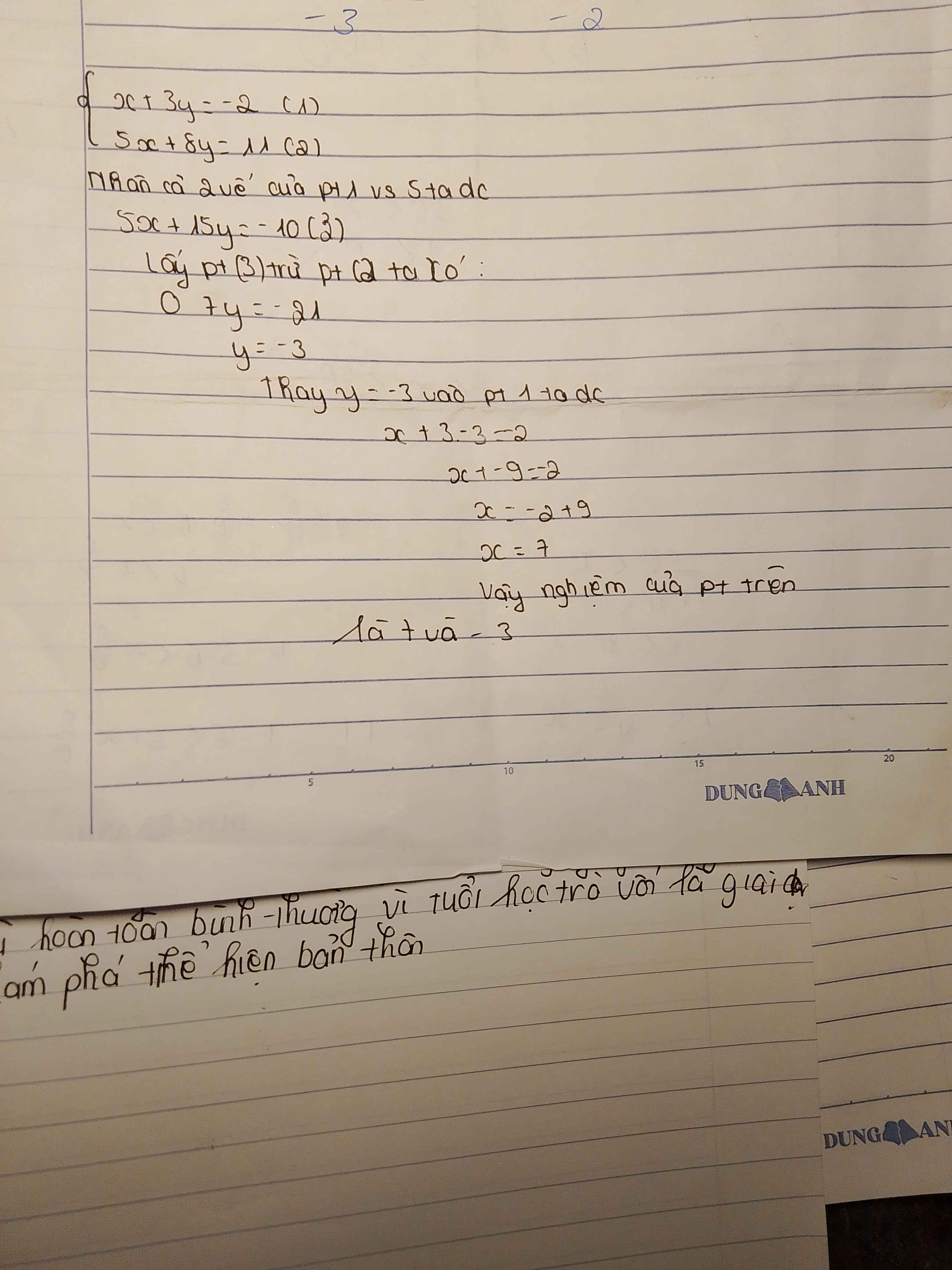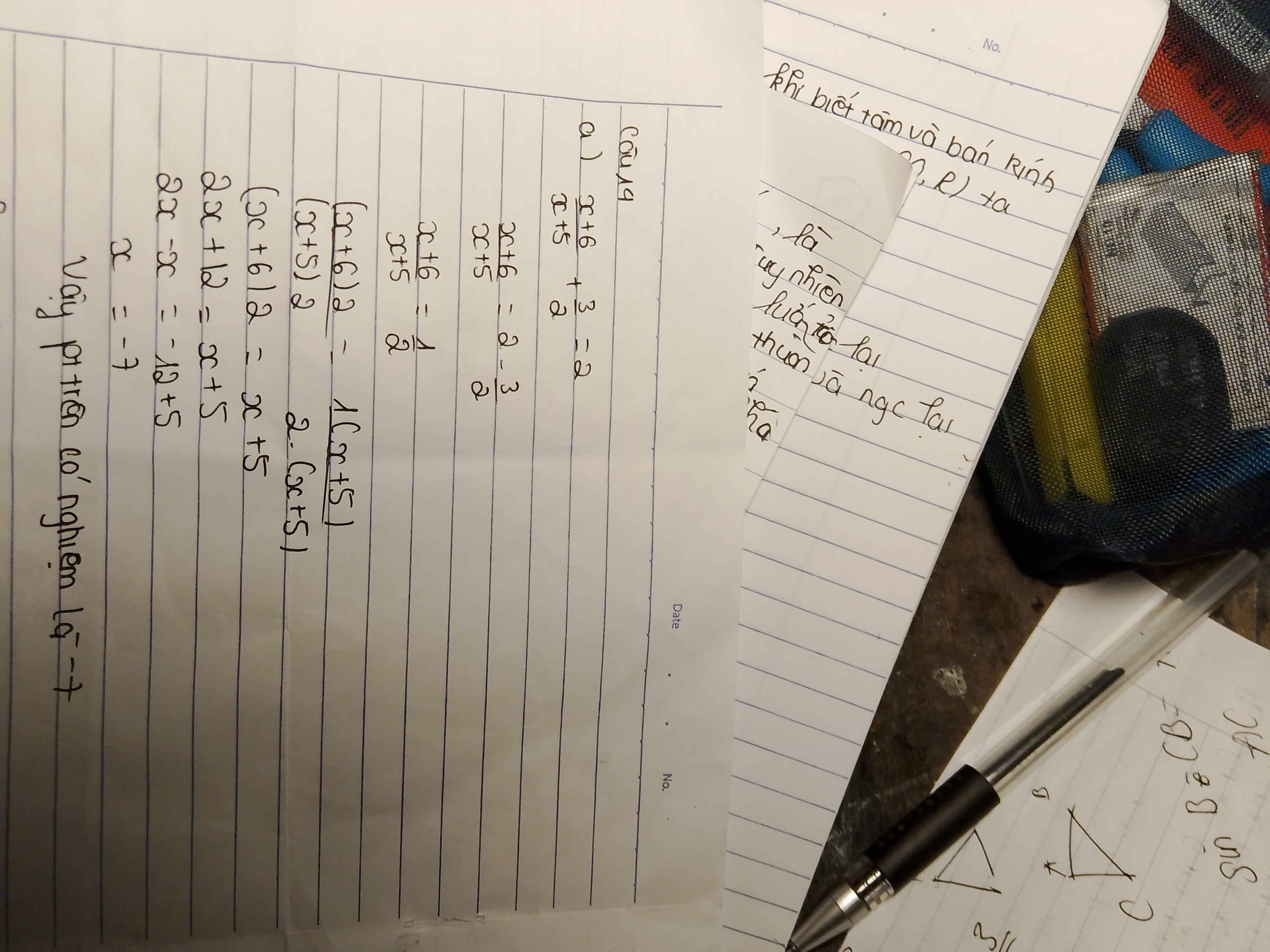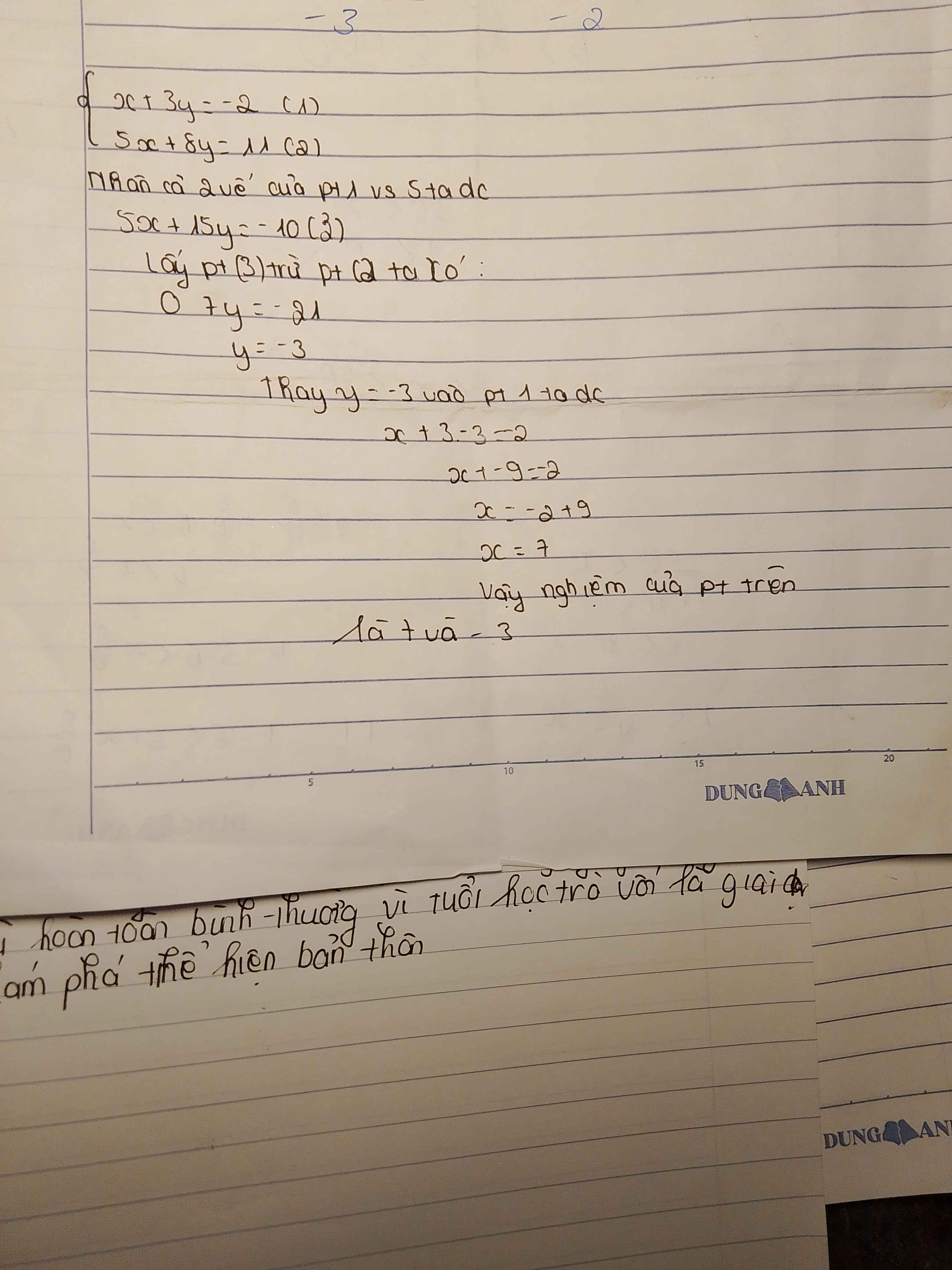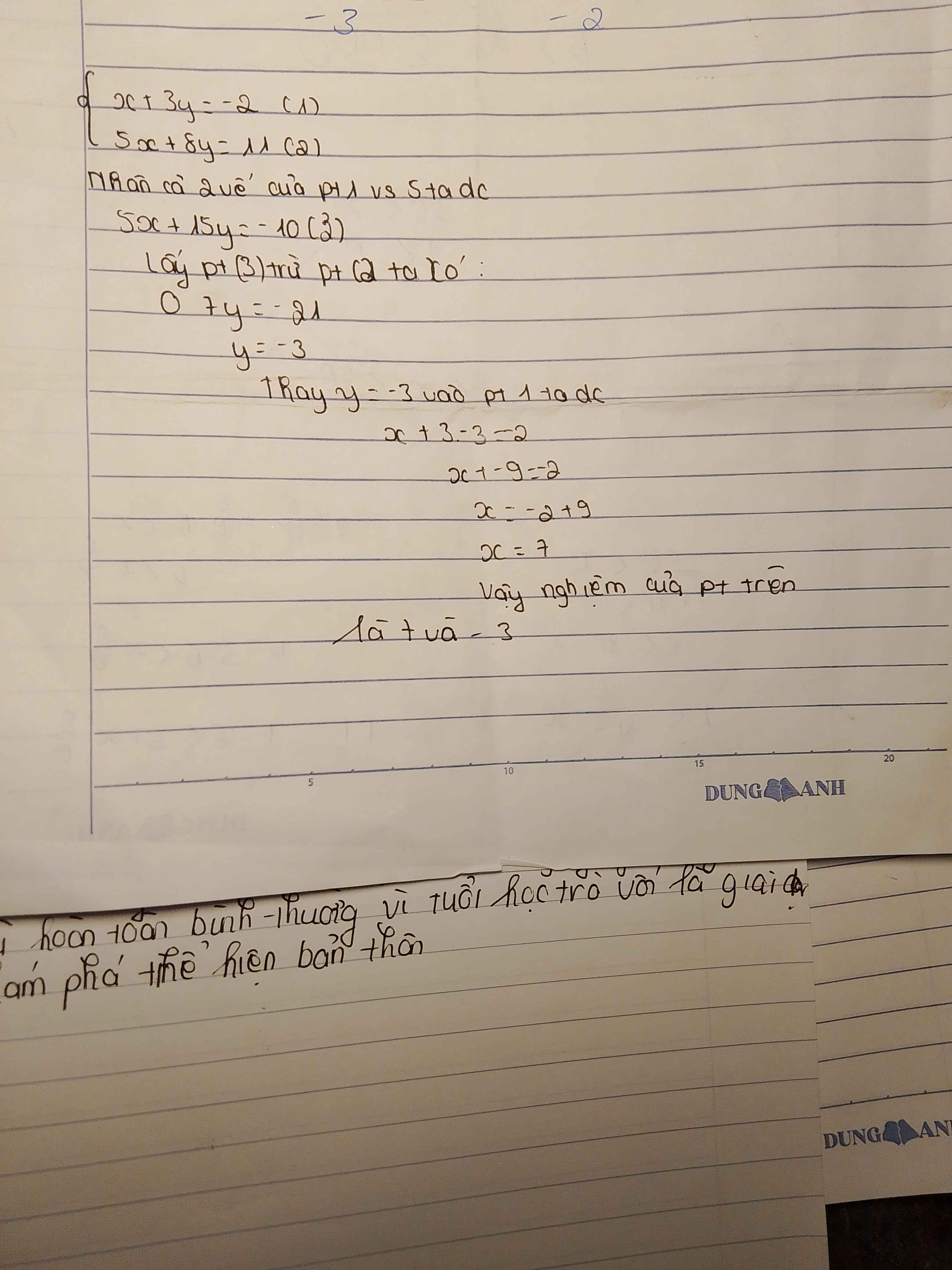Xét ∆ABC vuông tại B, ta có:

tanBAC=BC/AB(tỉ số lượng giác của góc nhọn)

=2/2,5

=0,8

 ⇒BAC≈38,7

Ta có:  BAD=BAC+CAD

=38,7+20

=58,7

Xét ∆ABD vuông tại B, ta có: 

tanBAD=BD/AB(tỉ số lượng giác của góc nhọn)

⇒BD=AB.tanBAD

=2,5.tan58,7

≈4,1m

⇒CD=BD−BC

=4,1−2

=2,1m

Vậy độ dài vùng được chiếu sáng trên mặt đất là 2,1m

1) +)Ta có:

sin35⁰ = cos(90⁰ - 35⁰) 

            = cos 55°

Vậy sin35⁰ = cos55⁰

+)Ta có:

tan35⁰ = cot(90⁰ - 35⁰)

             =cot 55°

Vậy tan35⁰ = cot55⁰

2)Xét ∆ABC vuông tại A 

⇒ AB = BC.cosB

= 20.cos36⁰

≈ 16,18 (cm)

Gọi vận tốc lúc về của người đó là x (x>0) (km/h)

Thì vận tốc lúc đi của người đó là: x+10 (km/h)

Thời gian người đó lúc về: 60/x(h)

Thời gian người đó lúc đi: 60/(x+10)(h)

Vì khi đi từ B về A, do trời mưa nên người đó giảm tốc độ 10km/h so với lúc đi nên thời gian về nhiều hơn thời gian đi là 30'(=1/2 h) nên ta có pt:

60/x - 60/(x + 10)  = 1/2

120(x + 10) - 120x = x(x + 10)
 120x + 1200 - 120x = x^2 + 10x
 x^2 + 10x - 1200 = 0
 x^2 - 30x + 40x - 1200 = 0
x(x - 30) + 40(x - 30) = 0

 (x - 30)(x + 40) = 0

Để giải pt đã cho ta giải 2 pt sau:

+)x-30=0.                                 +)x+40=0

     x=30(tm).                           x=-40(ktm)

Vậy tốc độ lúc về của người đó là 30km/h