

Lù Hoàng Lâm
Giới thiệu về bản thân



































Nối và . Kẻ ().
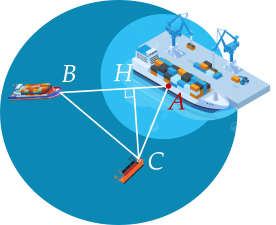
Sau giờ tàu chạy được quãng đường là: (hải lí).
Sau giờ tàu chạy được quãng đường là: (hải lí).
Xét tam giác vuông tại , ta có:
(hải lí).
(hải lí).
Do đó (hải lí).
Mặt khác, tam giác vuông tại , áp dụng định lí Pythagore ta có:
(hải lí).
Vậy sau giờ tàu cách tàu là hải lí.
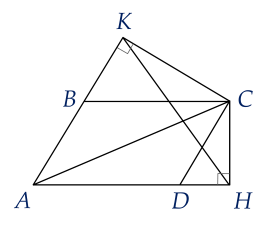
a) (g. g)
Vì
(cùng bằng )
hay (*)
Xét tứ giác có: ;
Suy ra: (**)
Từ (*) và (**) suy ra: (c-g-c)
b) suy ra
mà (cặp góc đồng vị) nên
Gọi (đồng) lần lượt là giá niêm yết của mỗi mặt hàng và
Một khách hàng mua hai món hàng và một món hàng thì phải trả số tiền là đồng nên ta có:
hay (1)
Trong khung giờ vàng khách hàng mua ba món hàng và hai món hàng trong khung giờ vàng nên phải trả số tiền là đồng nên ta có:
hay (2)
Từ (1) và (2) ta có hệ phương trình:
Giải hệ phương trình ta được:
Vậy giá niêm yết của mặt hàng là đồng, mặt hàng là đồng.
a) Ta có
+ Giải phương trình
+ Giải phương trình
Vậy phương trình có hai nghiệm là và .
b) Ta có:
Vậy hệ phương trình đã cho có nghiệm .
Gọi tốc độ của ca nô khi nước yên lặng là (km/h) ( ).
Tốc độ ca nô đi xuôi dòng là (km/h)
Ta có nên , tức là
Gọi (km) là quãng đường ca nô đi được trong giờ phút giờ
Ta có (km).
Do nên hay
Vậy quãng đường ca nô đi được trong giờ phút không vượt quá km.