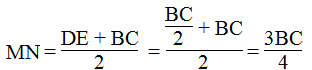Trong $\Delta$ABC ta có E là trung điểm của cạnh AB

D là trung điểm của cạnh AC nên ED là đường trung bình của $\Delta$ABC

⇒ ED//BC và ED = 1/2 BC

Tứ giác BCDE có ED//BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC//DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

=> Nên MN là đường trung hình hình thang BCDE => MN//DE

Trong $\Delta$BED, ta có: M là trung điểm BE

MI // DE

=> MI là đường trung bình của $\Delta$BED

=> MI = (1/2)DE = (1/4)BC

Trong $\Delta$CED ta có: N là trung điểm CD, NK // DE

=> NK là đường trung bình của $\Delta$CED

=> NK = (1/2)DE = (1/4)BC

IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC

=> MI = IK = KN = 1/4 BC

a) Ta có GM=1/2 GB

GD=1/2GB \\\ suy ra GM=GD ta có GN=1/2GC

GE=1/2GC vậy tứ giác MNDE có GM=GD và GN=GE nên là hình bình hành(vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường) => MN//DE , ND//ME (tích chất hình bình hành)

b) Tam giác ABC có NA = NB; MA = MC

=> NM là đường trung bình

=> MN // BC;  MN = 1/2 BC   (1)

  Tam giác GBC có: DG = DB;  EG = EC

=> ED  là đường trung bình

=>  ED // BC; ED = 1/2 BC

Từ (1) và (2) suy ra: MN // DE;  MN = ED

=> NMED là hình bình hành

=>  ME // ND

a/ Goi E là trung điểm  điểm của MC

Từ gt ��=12��⇒��=��=��AM=

​MC=>AM=ME=EC

Xét tg BCM có ME=EC; DB=DC => DE là đường trung bình của tg BCM => DE//BM 

Xét tg ADE có:

AM=ME, BM//DE =>OM//DE => OA=OD => O là trung điểm của AD

b/ Ta có DE là đường trung bình của tg BCM ⇒��=12��=>DE=
​BM

Xét tg ADE có

OA=OD; AM=ME => OM là đường trung bình của tg ADE

⇒��=12��=12.12��=14��=> OM=

​1/2(DE)=
​1/2.

​(1/2)BM=

​(1/4)BM

Gọi K là trung điểm của CD

a) Xét ΔBDC có 

M là trung điểm của BC

K là trung điểm của CD

Do đó: MK là đường trung bình =>MK//BD hay ID//MK

Xét ΔAMK có I là trung điểm của AM, ID//MK. Do đó: D là trung điểm của AK

=>AD=DK=KC

=>AD=1/2DC

b) Xét ΔAMK có 

I là trung điểm của AM

D là trung điểm của AK

Do đó: ID là đường trung bình =>ID=MK/2 hay MK=2ID

Ta có: MK là đường trung bình của ΔBDC nên MK=BD/2 =>BD/2=2ID hay BD=4ID