Ta có khoảng vân \(i=\dfrac{\lambda D}{a}=\dfrac{0,6.10^{-3}.2.10^3}{1}=1,2\left(mm\right)\)

Vân sáng thứ 3 cách vân sáng trung tâm một khoảng bằng \(x=3i=3,6mm\)

 \(\Rightarrow\) Chọn B

n=int(input('n=?'))

S=0

for i in range (1,n):

      if i%10==0:

          S=S+i

print('Tổng S các số tự nhiên nhỏ hơn',n,'chia hết cho 2 và 5 là',S)

Dự đoán KQ chạy:

1

2

3

4

5

 Code Python:

a=float(input('a=?'))

print('|',a,'|=',abs(a))

 a) Ta có \(W_{t_{đầu}}=mgh=0,2.10.10=20\left(J\right)\)

Vận tốc của vật khi chạm đất là \(v=\sqrt{2gh}=\sqrt{2.10.10}=10\sqrt{2}\left(m/s\right)\)

\(\Rightarrow W_{đ_{chạmđất}}=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,2.\left(10\sqrt{2}\right)^2=20\left(J\right)\)

Ta thấy \(W_{t_{đầu}}=W_{đ_{chạmđất}}=20J\)

 b) Cơ năng của vật là \(W=W_{t_{đầu}}+W_{đ_{đầu}}\) \(=20J\) (vì \(v_0=0\left(m/s\right)\))

Gọi vị trí mà động năng bằng thế năng là \(A\)

 \(\Rightarrow W_{t_A}=W_{đ_A}\) 

 \(\Rightarrow W_{t_A}=\dfrac{1}{2}W_A=\dfrac{1}{2}W=10J\)

 \(\Rightarrow mgh_A=10J\) 

 \(\Rightarrow0,2.10h_A=10J\)

 \(\Rightarrow h_A=5\left(m\right)\)

 Vậy khi vật ở độ cao 5m so với mặt đất thì động năng bằng thế năng.

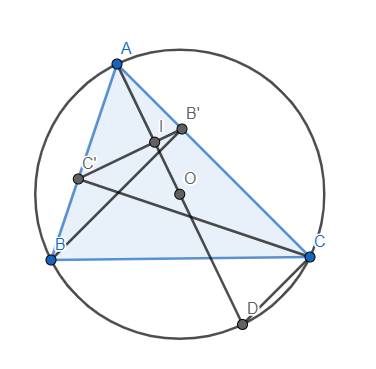
 a) Tứ giác BCB'C' có \(\widehat{BC'C}=\widehat{BB'C}=90^o\) nên nó là tứ giác nội tiếp (2 đỉnh kề nhau nhìn cạnh đối diện dưới 2 góc bằng nhau)

 b) Vì tứ giác BCB'C' nội tiếp nên \(\widehat{AB'C'}=\widehat{ABC}\) (góc ngoài bằng góc trong đối)

 Xét tam giác AB'C' và tam giác ABC có:

 \(\widehat{BAC}\) chung và \(\widehat{AB'C'}=\widehat{ABC}\)

 \(\Rightarrow\Delta AB'C'\sim\Delta ABC\left(g.g\right)\)

c) Theo câu b), ta có \(\widehat{AB'I}=\widehat{ABC}\)

Lại có \(\widehat{ABC}=\widehat{ADC}\) (góc nội tiếp cùng chắn cung AC)

\(\Rightarrow\widehat{AB'I}=\widehat{ADC}\) \(\Rightarrow\) Tứ giác B'IDC nội tiếp (góc ngoài bằng góc trong đối)

Đk: \(x\ge0\)

pt đã cho \(\Leftrightarrow6\sqrt{2x+7}-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)=2\sqrt{x}-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)\)

\(\Leftrightarrow\dfrac{36\left(2x+7\right)-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)^2}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)^2}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{72x+252-\dfrac{9}{4}x^2-\dfrac{99}{2}x-\dfrac{1089}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\dfrac{1}{4}x^2-\dfrac{3}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{-\dfrac{9}{4}x^2+\dfrac{45}{2}x-\dfrac{81}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{-\dfrac{1}{4}x^2+\dfrac{5}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{x^2-10x+9}{-\dfrac{4}{9}\left(6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}=\dfrac{x^2-10x+9}{-4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\)

\(\Leftrightarrow\left(x^2-10x+9\right)\left[\dfrac{9}{4\left(6+\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}-\dfrac{1}{4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-10x+9=0\\\dfrac{9}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{1}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\end{matrix}\right.\)

Với \(x^2-10x+9=0\Leftrightarrow\left(x-1\right)\left(x-9\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\) (nhận)

pt nhỏ thứ 2 \(\Leftrightarrow18\sqrt{x}+\dfrac{9}{2}x+\dfrac{27}{2}=6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\)

\(\Leftrightarrow6\sqrt{2x+7}-18\sqrt{x}=3x-3\)

\(\Leftrightarrow2\sqrt{2x+7}-6\sqrt{x}=x-1\)

\(\Leftrightarrow\dfrac{4\left(2x+7\right)-36x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)

\(\Leftrightarrow\dfrac{28-28x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)

\(\Leftrightarrow\left(x-1\right)\left(1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}=0\left(loại\right)\end{matrix}\right.\)

Vậy pt đã cho có tập nghiệm \(S=\left\{1;9\right\}\)