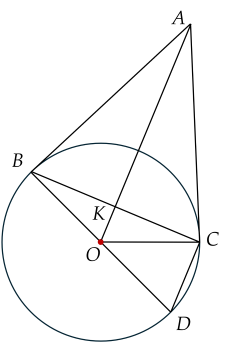
a) Xét tam giác $ABC$ có $AB=AC$ và $AO$ là đường phân giác của góc $BAC$ (tính chất hai tiếp tuyến cắt nhau). Do đó $AO$ cũng là đường cao, đường trung tuyến của $\Delta BAC$.

Vậy $AO$ vuông góc với $BC$.

b) Ta có BDC^=12CB⌢\(\widehat{BDC}=\dfrac{1}{2}\stackrel\frown{CB}\text{ (góc nội tiếp)}\)

\(\widehat{BOC}=\stackrel\frown{CB}\text{(góc ở tâm)}\)

Mặt khác \(\widehat{BAC}=\dfrac{1}{2}\widehat{BOC}\) nên \(\widehat{BAC}=\dfrac{1}{2}\stackrel\frown{CB}\)

Vậy \(\widehat{BAC}=\widehat{BDC}\) ,suy ra OA//CD (hai góc đồng vị bằng nhau).

c) Xét tam giác $ABO$ và tam giác $BKO$ có:

\(\widehat{ABO}=\widehat{BKO}=90^{\text{∘}}\)

\(\widehat{BOA}:\text{ góc chung }\)

Suy ra $\Delta ABO\sim \Delta BKO$ (g.g).

Do đó ta có tỉ số\(\dfrac{AO}{BO}=\dfrac{BO}{KO}\text{hay O A . O K = O B ^2 = 6 ^2 = 36 (cm).}\)

Xét tam giác vuông $ABO$ có: \(\sin\widehat{BAO}=\dfrac{OB}{OA}=\dfrac{6}{12}\) 

Suy ra \(\widehat{BAO}=30^{\text{∘}}\)

Gọi $x$ là số máy in mà nhà xuất bản sử dụng $(1\le x\le 14)$.

Chi phí lắp đặt là $120x$ (nghìn đồng).

Số giờ để sản xuất đủ số ấn phẩm là\(\dfrac{4000}{30x}\text{(giờ).}\)

Chi phí giám sát là: 90.400030x=12000x90
​\(.\dfrac{4000}{30x}=\dfrac{12000}{x}\) (nghìn đồng).

Chi phí sản xuất của nhà sản xuất là: A=120x+12000xA=120x+\(\dfrac{12000}{x}\)

​ (nghìn đồng).

Áp dụng bất đẳng thức Cauchy, ta có:

\(A=120x+\dfrac{12000}{x}\ge2\sqrt{120x.\dfrac{12000}{x}=2400}\)

Dấu bằng xảy ra khi $120x=$\(\dfrac{12000}{x}\) hay $x=10$.

Vậy số máy in nhà xuất bản nên sử dụng để chi phí in là nhỏ nhất là $10$ máy.

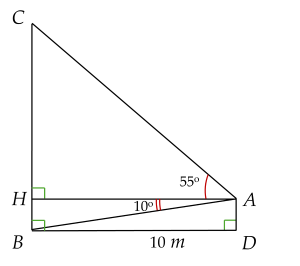
Dựa vào hình vẽ minh họa, ta có: $AH=BD=10$ m.

Xét $\Delta AHB$ vuông tại $H$, ta có:

\(\tan\widehat{BAH}=\dfrac{BH}{AH}\)(tỉ số lượng giác của góc nhọn)

suy ra BH=AH.tan⁡BAH^=10.tan⁡10∘BH=AH.tan\(\widehat{BAH}=10.\tan10^{\text{∘}}\)
 (m).

Xét $\Delta AHC$ vuông tại $H$, ta có:

\(\tan\widehat{CAH}=\dfrac{CH}{AH}\)(tỉ số lượng giác của góc nhọn)

suy ra $CH=AH.\backslash (\backslash tan\backslash widehat\{CAH\}=10.\backslash tan55^\{\backslash text\{\circ \; \}\}\backslash text\{(m)\; \}\backslash )$

Ta có:\(BC=BH+CH=10.\tan10^{\text{∘ }}+10.\tan55^{\text{∘ }}\)\(\approx16m\)

Vậy chiều cao của tháp là $16$ m.

Đổi $1$ giờ $25$ phút= \(\dfrac{17}{12}giờ,1giờ30\text{phút}=\dfrac{3}{2}giờ\)=1712

Gọi vận tốc riêng của ca nô và vận tốc của dòng nước lần lượt là $x$ (km/h) và $y$ (km/h). Điều kiện $x>0,y>0,x>y$.

Trong lần 1

+) Vận tốc xuôi dòng là $x+y$ km/h, quãng đường xuôi dòng là $20$ km nên thời gian xuôi dòng là\(\dfrac{20}{x+y}\left(\text{giờ}\right)\)

+) Vận tốc ngược dòng là $x-y$ km/h, quãng đường ngược dòng là $18$ km nên thời gian ngược dòng là\(\dfrac{18}{x-y}\) 18x−y
​ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết\(\dfrac{17}{12}\) 1712

​ giờ nên ta có phương trình

\(\dfrac{20}{x+y}+\dfrac{18}{x-y}=\dfrac{17}{12}\)(1)

Trong lần 2

+) Vận tốc xuôi dòng là $x+y$ (km/h), quãng đường xuôi dòng là $15$ km nên thời gian xuôi dòng là \(\dfrac{15}{x+y}\left(giờ\right)\)15x+y

 (giờ).+) Vận tốc ngược dòng là $x-y(km/h)$, quãng đường ngược dòng là $24$ km nên thời gian ngược dòng là\(\dfrac{24}{x-y}\) 24x−y

​ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết 32\(\dfrac{3}{2}\) giờ nên ta có phương trình\(\dfrac{15}{x+y}+\dfrac{24}{x-y}=\dfrac{3}{2}\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình

\(\left\{{}\begin{matrix}\dfrac{20}{x+y}+\dfrac{18}{x-y}=\dfrac{17}{12}\\\dfrac{15}{x+y}+\dfrac{24}{x-y}=\dfrac{3}{2}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{54}{x-y}=\dfrac{17}{4}\\\dfrac{60}{x+y}+\dfrac{94}{x-y}=\dfrac{7}{4}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{54}{x-y}=\dfrac{17}{4}&\dfrac{42}{x-y}=\dfrac{7}{4}&\end{matrix}\right.\)

Quy đồng ta được hệ \(\left\{{}\begin{matrix}\text{x+y=30 ​ }\\x−y=24\end{matrix}\right.\)

Giải hệ trên, ta được: \(\left\{{}\begin{matrix}x=27\\y=3\end{matrix}\right.\)(thỏa mãn điều kiện).

{x=27y=3

{20x+y+18x−y=171215x+y+24x−y=32

a. Rút gọn biểu thức $A$.

\(A=\left(\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{2-\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\right):\left(2-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)

\(A=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\right):\left(2-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)

\(A=\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)

\(A=\dfrac{1}{\sqrt{x}-2}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)

\(A=\dfrac{\sqrt{x}+1}{x-4}\)

b. Tìm các giá trị của x để 1A≤−52 \(\dfrac{1}{A}\le-\dfrac{5}{2}\)

\(\left\{ĐK:x\ge0,x\ne4,x=9\right\}\)

Để \(\dfrac{1}{A}\le-\dfrac{5}{2}\) thì

\(\dfrac{x-4}{\sqrt{x}+1}\le-\dfrac{5}{2}\)

\(2x-8\le-5\sqrt{x}-5\)

\(2x+5\sqrt{x}-3\le0\)

\(-3\le\sqrt{x}\le\dfrac{1}{2}\)

\(0\le\sqrt{x}\le\dfrac{1}{2}\)

\(0\le x\le\dfrac{1}{4}\)

Kết hợp với điều kiện ta được 0≤x≤14\(0\le x\le\dfrac{1}{4}\) thì\(\dfrac{1}{A}\le-\dfrac{5}{2}\)

\(A=\sqrt{2-\sqrt{3}}.\left(\sqrt{6}+\sqrt{2}\right)\)

\(A=\sqrt{2}.\left(\sqrt{2-\sqrt{3}}\right)+\sqrt{6}.\left(\sqrt{2-\sqrt{3}}\right)\)

\(A=\sqrt{4-2\sqrt{3}}+\sqrt{12-6\sqrt{3}}\)

\(A=\sqrt{1+3-2\sqrt{1.3}}+\sqrt{12-2.3\sqrt{3}}\)

\(A=\sqrt{1^2-2\sqrt{1.3}+\left(\sqrt{3}\right)^2}+\sqrt{3^2-2.3\sqrt{3}+\left(\sqrt{3}\right)^2}\)

\(A=\sqrt{1^2-\left(\sqrt{3}\right)^2}+\sqrt{\left(3-\sqrt{3}\right)^2}\)

\(A=\sqrt{3}-1=3-\sqrt{3}=2\)

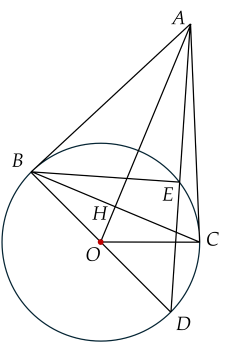
a) Xét đường tròn $(O)$ có: $AB$, $AC$ lần lượt là tiếp tuyến tại $B,C$ nên $AB=AC$ (tính chất hai tiếp tuyến cắt nhau) .

Suy ra $A$ thuộc đường trung trực của $BC$.

Mà $OB=OC=R$ nên $O$ thuộc đường trung trực của $BC$

Do đó $OA$ là đường trung trực của $BC$ nên $OA\perp BC$ tại $H$.

b) Xét tam giác $BED$ có $OE$ là trung tuyến. Mặt khác OE=BD2OE=\(\dfrac{BD}{2}\)

​ nên tam giác $BED$ vuông tại $E$.

Xét $\Delta ABE$ và $\Delta ABD$ có:

\(\widehat{BAD}\)  góc chung

\(\widehat{BEA}=\widehat{DBA}=90^{\text{∘}}\)

Suy ra $\Delta ABE\sim \Delta ADB$ (g.g)

Khi đó ABE^=ADB^\(\widehat{ABE}=\widehat{ADB}\) (hai góc tương ứng)

và \(\dfrac{AB}{AD}=\dfrac{AE}{AB}\text{ ​ hay A B^2 = A D . A E (đpcm).}\)ABAD=AEAB

​.c) Xét tam giác vuông $AOB$ có:

\(\cos\widehat{AOB}=\dfrac{OB}{OA}=\dfrac{1}{\sqrt{6}+\sqrt{2}}\)

Suy ra \(\widehat{AOB}=75^{\text{∘}}.Dođo\widehat{BOC}=150^{\text{∘}}\)

Khi đó \(\widehat{COD}=30^{\text{∘}}\)

Diện tích hình quạt giới hạn bởi bán kính $OC$, $OD$ và cung nhỏ $CD$ là:

\(S=\dfrac{\pi R^2.30}{360}=\dfrac{\pi R^2}{12}\left(đvdt\right)\)

Vậy diện tích hình quạt giới hạn bởi bán kính $OC$, $OD$ và cung nhỏ $CD$ là\(\dfrac{\pi R^2}{12}\left(đvdt\right)\)

​Gọi $x$ là số ti vi mà cửa hàng đặt mỗi lần ($x\in [1;2500]$, đơn vị cái).

Số lượng ti vi trung bình gửi trong kho là ​\(\dfrac{x}{2}\) nên chi phí lưu kho tương ứng làx2

    10.x2=5x10.\(\dfrac{x}{2}\text{=5x}\)

($)$(\$)$

Số lần đặt hàng mỗi năm là 2500x\(\dfrac{2500}{x}\) và chi phí đặt hàng là:\(\dfrac{2500}{x}\)​.​(20+9x) $(\$)$

Khi đó chi phí mà cửa hàng phải trả là:

$C(x)=$​\(\dfrac{2500}{x}\).(20+9x)+5x=5x+\(\dfrac{50000}{x}\)+22500
​Ta có $5x+$​\(\dfrac{50000}{x}\)≤ 2\(\sqrt{5x.\dfrac{50000}{x}}=1000\) 

Suy ra $C(x)\le 23500$. Dấu $"="$ xảy ra khi 5x=50000x5x=\(\dfrac{50000}{x}\)

​, khi đó $x=100$.

Vậy mỗi năm, cửa hàng nên đặt $100$ cái ti vi để chi phí hàng tồn kho là nhỏ nhất.

Gọi số học sinh dự thi của trường A và trường B lần lượt là $x$ và $y$ (học sinh). Điều kiện: x,y∈N∗.x,y∈\(ℕ^∗\).

Do cả hai trường có $840$ học sinh thi đỗ vào lớp $10$ và đạt tỉ lệ thi đỗ là $84\%$ nên ta có phương trình:

$84\%.(x+y)=840$ hay $x+y=1000$ (1)

Vì trường A tỉ lệ thi đỗ là $80\%$, trường B tỉ lệ thi đỗ là $90\%$ nên ta có phương trình:

$80\%.x+90\%.y=840$

$0,8x+0,9y=840$

$8x+9y=8400$ (2)

Từ $(1)$ và $(2)$ ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=1000\\8x+9y=8400\end{matrix}\right.\)

\(\left\{{}\begin{matrix}9x+9y=9000\\8x+0y=8400\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=600\\y=400\end{matrix}\right.\)(thỏa mãn đk)

Vậy số học sinh dự thi của trường A và trường B lần lượt là $600$ và $400$ (học sinh).

a)

Xét $\Delta ABC$ vuông tại $A$, ta có:

\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{320}=\dfrac{3}{80}\)

Suy ra  \(\widehat{B}\approx\text{2 ∘ 9 ′ .}\)

Vậy góc nghiêng là 2∘ 9′\(\text{ 2∘ 9 ′ .}\)

b)

Xét $\Delta ABC$ vuông tại $A$, ta có:

\(BC=\dfrac{AC}{\sin\widehat{B}}=\dfrac{12}{\sin5^{\text{∘ }}}\approx137,7km\)

Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay $137,7$ km