

Cao Duy Anh
Giới thiệu về bản thân



































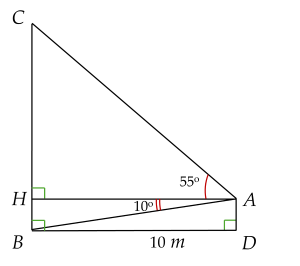
Dựa vào hình vẽ minh họa, ta có: m.
Xét vuông tại , ta có:
(tỉ số lượng giác của góc nhọn)
suy ra (m).
Xét vuông tại , ta có:
(tỉ số lượng giác của góc nhọn)
suy ra (m).
Ta có:
Đổi giờ phút giờ; giờ phút giờ.
Gọi vận tốc riêng của ca nô và vận tốc của dòng nước lần lượt là (km/h) và (km/h). Điều kiện .
Trong lần 1
+) Vận tốc xuôi dòng là km/h, quãng đường xuôi dòng là km nên thời gian xuôi dòng là (giờ).
+) Vận tốc ngược dòng là km/h, quãng đường ngược dòng là km nên thời gian ngược dòng là (giờ).
Vì tổng thời gian xuôi dòng và ngược dòng hết giờ nên ta có phương trình
(1)
Trong lần 2
+) Vận tốc xuôi dòng là (km/h), quãng đường xuôi dòng là km nên thời gian xuôi dòng là (giờ).
+) Vận tốc ngược dòng là , quãng đường ngược dòng là km nên thời gian ngược dòng là (giờ).
Vì tổng thời gian xuôi dòng và ngược dòng hết giờ nên ta có phương trình
(2)
Từ (1) và (2) ta có hệ phương trình
Quy đồng ta được hệ
Giải hệ trên, ta được: (thỏa mãn điều kiện).
Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là km/h và km/h.
Đổi giờ phút giờ; giờ phút giờ.
Gọi vận tốc riêng của ca nô và vận tốc của dòng nước lần lượt là (km/h) và (km/h). Điều kiện .
Trong lần 1
+) Vận tốc xuôi dòng là km/h, quãng đường xuôi dòng là km nên thời gian xuôi dòng là (giờ).
+) Vận tốc ngược dòng là km/h, quãng đường ngược dòng là km nên thời gian ngược dòng là (giờ).
Vì tổng thời gian xuôi dòng và ngược dòng hết giờ nên ta có phương trình
(1)
Trong lần 2
+) Vận tốc xuôi dòng là (km/h), quãng đường xuôi dòng là km nên thời gian xuôi dòng là (giờ).
+) Vận tốc ngược dòng là , quãng đường ngược dòng là km nên thời gian ngược dòng là (giờ).
Vì tổng thời gian xuôi dòng và ngược dòng hết giờ nên ta có phương trình
(2)
Từ (1) và (2) ta có hệ phương trình
Quy đồng ta được hệ
Giải hệ trên, ta được: (thỏa mãn điều kiện).
Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là km/h và km/h.
.
b. Tìm các giá trị của x để .
(ĐK: )
Để thì
.
Kết hợp với điều kiện ta được thì .
.
b. Tìm các giá trị của x để .
(ĐK: )
Để thì
.
Kết hợp với điều kiện ta được thì .
.
a)

Xét vuông tại , ta có:
Suy ra .
Vậy góc nghiêng là .
b)

Xét vuông tại , ta có:
km.
Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay km.
a)

Xét vuông tại , ta có:
Suy ra .
Vậy góc nghiêng là .
b)

Xét vuông tại , ta có:
km.
Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay km.
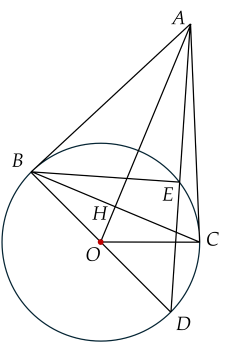
a) Xét đường tròn có: , lần lượt là tiếp tuyến tại nên (tính chất hai tiếp tuyến cắt nhau) .
Suy ra thuộc đường trung trực của .
Mà nên thuộc đường trung trực của
Do đó là đường trung trực của nên tại .
b) Xét tam giác có là trung tuyến. Mặt khác nên tam giác vuông tại .
Xét và có
: góc chung
Suy ra (g.g)
Khi đó (hai góc tương ứng)
và hay (đpcm).
c) Xét tam giác vuông có:
.
Suy ra . Do đó .
Khi đó .
Diện tích hình quạt giới hạn bởi bán kính , và cung nhỏ là:
(đvdt).
Vậy diện tích hình quạt giới hạn bởi bán kính , và cung nhỏ là (đvdt).

a) Xét đường tròn có: , lần lượt là tiếp tuyến tại nên (tính chất hai tiếp tuyến cắt nhau) .
Suy ra thuộc đường trung trực của .
Mà nên thuộc đường trung trực của
Do đó là đường trung trực của nên tại .
b) Xét tam giác có là trung tuyến. Mặt khác nên tam giác vuông tại .
Xét và có
: góc chung
Suy ra (g.g)
Khi đó (hai góc tương ứng)
và hay (đpcm).
c) Xét tam giác vuông có:
.
Suy ra . Do đó .
Khi đó .
Diện tích hình quạt giới hạn bởi bán kính , và cung nhỏ là:
(đvdt).
Vậy diện tích hình quạt giới hạn bởi bán kính , và cung nhỏ là (đvdt).