Có: 8/12 = 2/3 = 4/6
       35/30 = 7/6
Do đó: 8/12 < 35/30

90/540 = 1/6

Bài 5:

Xét △ABC vuông tại A có:

   \(\sin\widehat{ACB}=\dfrac{AB}{BC}\)(tỉ số lượng giác)

   ⇒ \(BC=\dfrac{AB}{\sin\widehat{ACB}}=\dfrac{3000}{\sin23^o}\approx7678\left(m\right)\)

Vậy máy bay phải bay một đoạn đường khoảng 7678m.

Bài 4:

 Tổng số tiền các món hàng khi chưa giảm giá là:

       2200000 + 12000000 + 1500000 = 15700000 (đồng)

 Tồng số tiền mà bác Đô phải trả khi giảm giá các món hàng là:

       15700000 - (15700000 * 12 : 100) - 300000 = 13516000 (đồng)

          Vậy bác Đô đã phải trả 13516000 đồng khi mua hàng.

Bài 3: 

a) 

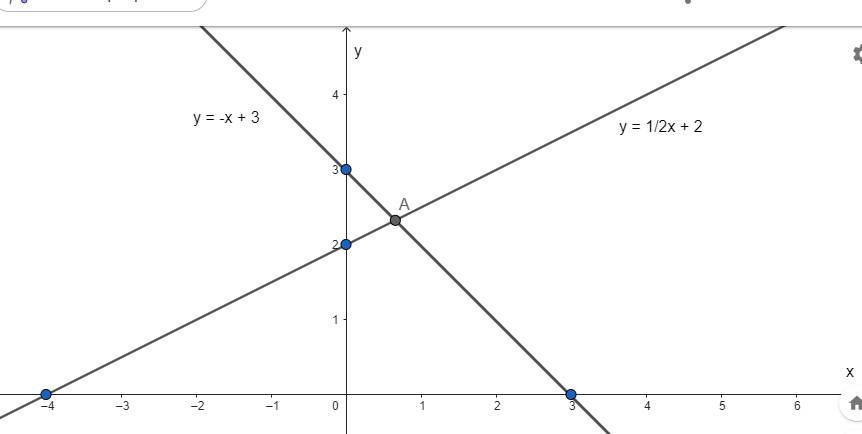
b) Xét phương trình hoành độ giao điểm của D₁ và D₂ có: y = y

  ⇒ \(\dfrac{1}{2}x+2=-x+3\)

  ⇒ \(\dfrac{3}{2}x=1\)

  ⇒ \(x=\dfrac{2}{3}\)

Thay \(x=\dfrac{2}{3}\) vào D₂ có \(y=-\dfrac{2}{3}+3=\dfrac{7}{3}\)

  ⇒ \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)

Vậy D₁ cắt D₂ tại \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)

c) ĐK: a ≠ 0

   Vì (D) // (D₂)

  ⇒ \(\left\{{}\begin{matrix}a=-1\left(TM\right)\\b\ne3\end{matrix}\right.\)

   Vì (D) cắt (D₁) tại điểm có hoành độ x = 2

   Tức là x = -2 và y = 1

   Thay x = 2; y = 0 và a = -1(TMĐK) vào D có:

  ⇒ \(-2\cdot-1+b=1\)

  ⇒ \(b+2=1\)

  ⇒ \(b=-1\left(TM\right)\)

Vậy (D) : y = \(-x-1\)

Bài 2:

a) \(\dfrac{5}{3}\sqrt{9x+18}+\dfrac{1}{2}\sqrt{4x+8}-15=\sqrt{2+x}\) (ĐKXĐ: x ≥ -2)

⇔ \(5\sqrt{x+2}+\sqrt{x+2}-\sqrt{x+2}=15\)

⇔ \(5\sqrt{x+2}=15\)

⇔ \(\sqrt{x+2}=3\)

⇔ \(x+2=9\)

⇔ \(x=7\left(TM\right)\)

Vậy S = {7}

b) \(\sqrt{x^2-4x+4}-6=2x\) (ĐKXĐ: x ≥ -3)

⇔ \(\sqrt{\left(x-2\right)^2}=2x+6\)

⇔ \(\left|x-2\right|=2x+6\)

⇔ \(\left\{{}\begin{matrix}x-2=2x+6\\x-2=-2x-6\end{matrix}\right.\)

⇔ ​\(\left\{{}\begin{matrix}x-2-2x-6=0\\x-2+2x+6=0\end{matrix}\right.\)​

⇔\(\left\{{}\begin{matrix}-x-8=0\\3x+4=0\end{matrix}\right.\)  ⇔ \(\left\{{}\begin{matrix}x=-8\left(KTM\right)\\x=-\dfrac{4}{3}\left(TM\right)\end{matrix}\right.\) 

Vậy S = \(\left\{-\dfrac{4}{3}\right\}\)

Bài 1:

a) \(\sqrt{20}+2\sqrt{45}-3\sqrt{80}+\sqrt{125}\)

  = \(2\sqrt{5}+6\sqrt{5}-12\sqrt{5}+5\sqrt{5}\)

  = \(\sqrt{5}\)

b) \(\dfrac{2\sqrt{3}+3\sqrt{2}}{\sqrt{3}+\sqrt{2}}-4\sqrt{\dfrac{3}{2}}-\dfrac{5}{1-\sqrt{6}}\)

  = \(\left(2\sqrt{3}+3\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)-2\sqrt{6}+1+\sqrt{6}\)

  = \(\sqrt{6}-\sqrt{6}+1=1\)

c) \(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4\left(\sqrt{x}-1\right)}{x-2\sqrt{x}}\) (ĐKXĐ: x > 0; x ≠ 4)

  = \(\dfrac{x-4\sqrt{x}+4}{x-2\sqrt{x}}\)

  = \(\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

  = \(\dfrac{\sqrt{x}-2}{\sqrt{x}}\)

Bài 4: \(\sqrt{x+3}\cdot x^4=2x^4-2023x+2023\) (ĐK: x ≥ -3)

       ⇔ \(x^4\left(\sqrt{x+3}-2\right)+2023\left(x-1\right)=0\)

      ⇔ \(x^4\left(\dfrac{x-1}{\sqrt{x+3}+2}\right)+2023\left(x-1\right)=0\)

      ⇔  \(\left(x-1\right)\left(\dfrac{x^4}{\sqrt{x+3}+2}+2023\right)=0\)

      ⇒ \(x-1=0\) 

      ⇔ \(x=1\left(TM\right)\)

Vậy S ∈ {1}

1) Xét △ABH vuông tại H có:

      \(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)

 ⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)

Vậy độ dài của mặt cầu trượt khoảng 4,5m.

2) 

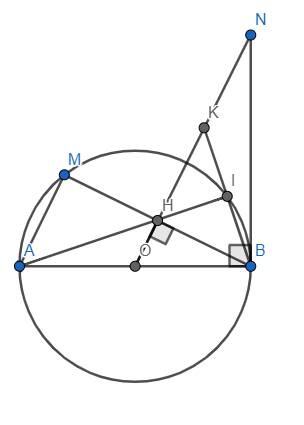
a) Xét △AMB có: A, M, B ∈ (O) (gt)

                              AB là đường kính của (O) (gt)

  ⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)

   Xét △AMB vuông tại M có: O là trung điểm AB(gt)

                                                  OH // AM (⊥ MB)

  ⇒ OH là đường trung bình của △AMB

  ⇒ H là trung điểm của MB (t/c)(đpcm)

  Xét △NMB có: H là trung điểm của MB(cmt)

                         NH ⊥ MB(do N ∈ OH ⊥ MB)

  ⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB

  ⇒ △NMB cân tại N(t/c △ cân)

  ⇒ NM = NB(t/c △ cân)

  Xét △NMO và △NBO có:

      ON chung

      NM = NB(cmt)

      OM = OB(= R)

  ⇒ △NMO = △NBO (c.c.c)

  ⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)

  ⇒ NM ⊥ MO

  Mà OM = R

  ⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)

b) Xét △MAB và △HBN có: 

     \(\widehat{AMB}=\widehat{BHN}=90^o\)

     \(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))

 ⇒ △MAB ∼ △HBN (g.g)(đpcm)