Bài học cùng chủ đề
- Trường hợp đồng dạng thứ nhất của tam giác (c.c.c)
- Trường hợp đồng dạng thứ hai của tam giác (c.g.c)
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Trường hợp đồng dạng thứ nhất của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ nhất của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ hai của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ hai của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
- Trường hợp bằng nhau thứ nhất của hai tam giác
- Trường hợp bằng nhau thứ hai của hai tam giác
- Trường hợp bằng nhau thứ ba của hai tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Trường hợp đồng dạng thứ hai của hai tam giác (cơ bản) SVIP
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc - cạnh nếu
Cho ΔDEF và ΔILK, biết DE=10 cm; EF=4 cm; IL=20 cm; LK=8 cm cần thêm điều kiện gì để ΔDEF∽ΔILK (c-g-c)?

Để hai tam giác ABC và DEF đồng dạng thì số đo D trong hình vẽ trên bằng
Cho hình vẽ:
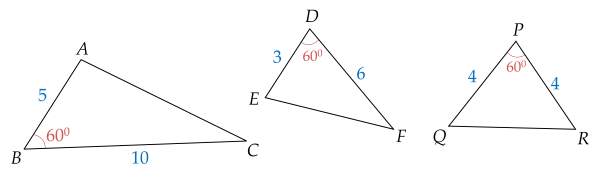
Khẳng định nào dưới đây đúng?
Cho ΔABC và ΔDEF có B=E, BCBA=EFDE thì
Cho ΔA′B′C′ và ΔABC có A=A′. Để ΔA′B′C′∽ΔABC cần thêm điều kiện là
Cho ΔMNP∽ΔKIH, biết MN=2 cm, MP=8 cm, KH=4 cm, thì KI bằng
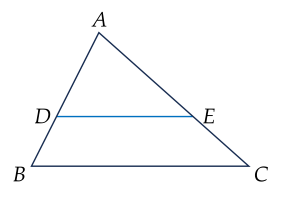
Cho ΔABC, lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho ABAD=ACAE.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) ABAE=ACAD. |
|
| b) ADE=ABC. |
|
| c) ΔADE∽ΔABC. |
|
| d) DE // BC. |
|
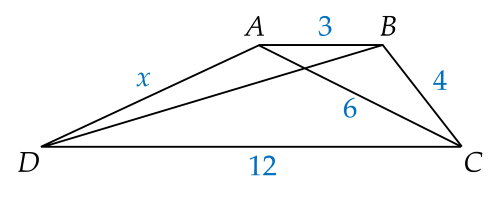
Với AB // CD, AB=3, BC=4, CD=12 và AC=6 thì giá trị của x trong hình vẽ dưới đây là
Cho ΔABC vuông tại A, đường cao AH(H∈BC).
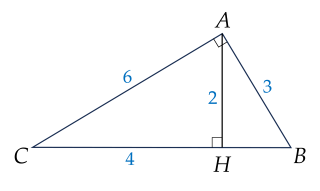
Biết AB=3 cm, AC=6 cm, AH=2 cm, HC=4 cm. Hệ thức nào sau đây đúng?
Tam giác ABC và tam giác AED trong hình trên có đồng dạng với nhau không?
Cho hình thang vuông ABCD, (A=D=90∘) có AB=16 cm, CD=25 cm, BD=20 cm.
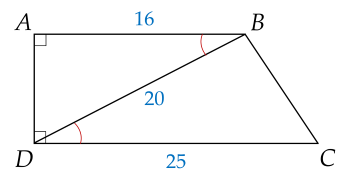
Độ dài cạnh BC là
Cho ΔMNP∽ΔEFH theo tỉ số k. Gọi MM′, EE′ lần lượt là hai trung tuyến của ΔMNP và ΔEFH. Khi đó ta chứng minh được
Cho hình vẽ:
Độ dài BC là
Cho hình thang ABCD (AB // CD) có AB=28 cm, DC=112 cm, BD=56 cm. Chứng minh BC=2AD.
Hoàn thành bài giải dưới đây:
Xét tam giác ABD và tam giác BDC có:
(Hai góc so le trong)
Suy ra ΔABD∽ΔBDC
Do đó, ADBC= = =
(Kéo thả hoặc click vào để điền)

Bạn có thể đăng câu hỏi về bài học này ở đây
