Bài học cùng chủ đề
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
- Trường hợp đồng dạng đặc biệt của tam giác vuông
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
- Các trường hợp đồng dạng của hai tam giác vuông (cơ bản)
- Các trường hợp đồng dạng của hai tam giác vuông (vận dụng)
- Trường hợp bằng nhau thứ ba của hai tam giác
- Các trường hợp đồng dạng của hai tam giác vuông
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản) SVIP
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
Nếu ΔABC và ΔDEF có A=D, C=F thì
Nếu ΔABC và ΔMNP có A=N; B=M thì
Nếu ΔABC và ΔDEF có A=70∘, C=60∘, E=50∘, F=70∘ thì
Nếu ΔABC và ΔFED có A=F, cần thêm điều kiện gì dưới đây để ΔABC∽ΔFED?
Cho ΔABC∽ΔA′B′C′ (g.g). Khẳng định nào sau đây đúng?
Cho hình vẽ, khẳng định nào sau đây đúng?
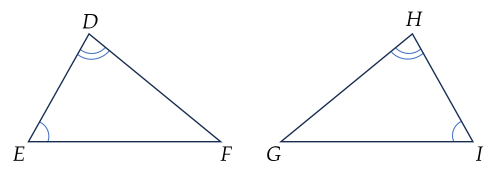
Nếu ΔMNP và ΔDEF có M=D=90∘, P=50∘. Để ΔMNP∽ΔDEF thì cần thêm điều kiện
Nếu ΔDEF và ΔSRK có D=70∘; E=60∘; S=70∘; K=50∘ thì
Cho hình vẽ. Khẳng định nào sao đây đúng
Cho tam giác FLG và tam giác CKM có L=M; G=C. Khẳng định nào sau đây đúng?
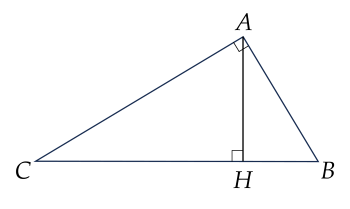
Cho ΔABC vuông tại A có AB=30 cm, AC=40 cm. Kẻ đường cao AH, (H∈BC). Độ dài đường cao AH là
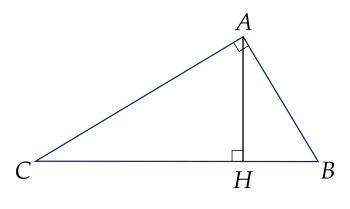
Cho ΔABC vuông tại A, đường cao AH.
(Nhấp vào dòng để chọn đúng / sai)| AH=CH.BH. |
|
| AB=BC.BH. |
|
| AH2=BH.CH. |
|
| AC2=CH.BH. |
|
Cho hình thang ABCD với AB // CD, O là giao điểm hai đường chéo AC và BD. Khẳng định nào sau đây đúng?
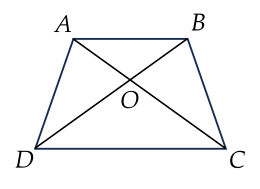
Cho hình thang ABCD có AB // CD, O là giao điểm hai đường chéo AC và BD. Khẳng định nào sau đây đúng?
Cho tam giác FKP có đường cao FN và KM cắt nhau tại E.
(Nhấp vào dòng để chọn đúng / sai)
| ΔKEN∽ΔFEM. |
|
| ΔFNP∽ΔKMP. |
|
| ΔFKE∽ΔFKM. |
|
| ΔFKM∽ΔKFN. |
|

Bạn có thể đăng câu hỏi về bài học này ở đây
