Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1 (2 điểm).
1) Thực hiện phép tính: $ \left( 3\sqrt{3}+2\sqrt{5} \right)\sqrt{3}-\sqrt{60}$.
2) Hàm số $ y=(2-\sqrt{3})x+2$ là hàm số đồng biến hay nghịch biến trên $\mathbb{R}$? Vì sao?
3) Rút gọn biểu thức $A=\left( \dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1} \right).\dfrac{5\sqrt{x}}{\sqrt{x}+1}$ (với $ x>0; \, x\ne 1$).
Hướng dẫn giải:
1) $ \left( 3\sqrt{3}+2\sqrt{5} \right)\sqrt{3}-\sqrt{60}=3.3+2\sqrt{15}-2\sqrt{15}$ $ =9$.
2) Hàm số $ y=(2-\sqrt{3})x+2$ có hệ số $ a=2-\sqrt{3}>0$ (vì $ 2=\sqrt{4}>\sqrt{3}$)
Vậy hàm số $ y=(2-\sqrt{3})x+2$ đồng biến trên $\mathbb{R}$.
3) Với $x>0, \, x\ne 1$, ta có $A=\left( \dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1} \right).\dfrac{5\sqrt{x}}{\sqrt{x}+1}$
$=\left( \dfrac{1}{\sqrt{x}(\sqrt{x}-1)}+\dfrac{\sqrt{x}}{\sqrt{x}\left( \sqrt{x}-1 \right)} \right).\dfrac{5\sqrt{x}}{\sqrt{x}+1}$
$=\dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)}.\dfrac{5\sqrt{x}}{\sqrt{x}+1}$
$=\dfrac{5}{\sqrt{x}-1}$.
Bài 2 (2 điểm). Cho hàm số bậc nhất $y=\left( m-2 \right)x+m+1$ (với $m$ là tham số, $m\ne 2$), có đồ thị là đường thẳng $(d)$.
1) Tìm $m$ để $(d)$ đi qua điểm $ A\left( 1;-1 \right)$.
2) Vẽ đồ thị hàm số với $m$ tìm được ở ý trên.
3) Tìm $m$ để đường thẳng $(d)$ song song với đường thẳng $ \left({d}' \right): \, y=1-3x$ .
Hướng dẫn giải:
1) Vì đường thẳng $(d) $ đi qua điểm $ A\left( 1;-1 \right)$ nên với $ x=1; \, y=-1$ ta có:
$ -1=\left( m-2 \right).1+m+1 \Leftrightarrow 2m=0\Leftrightarrow m=0$
Vậy $ m=0$ là giá trị cần tìm.
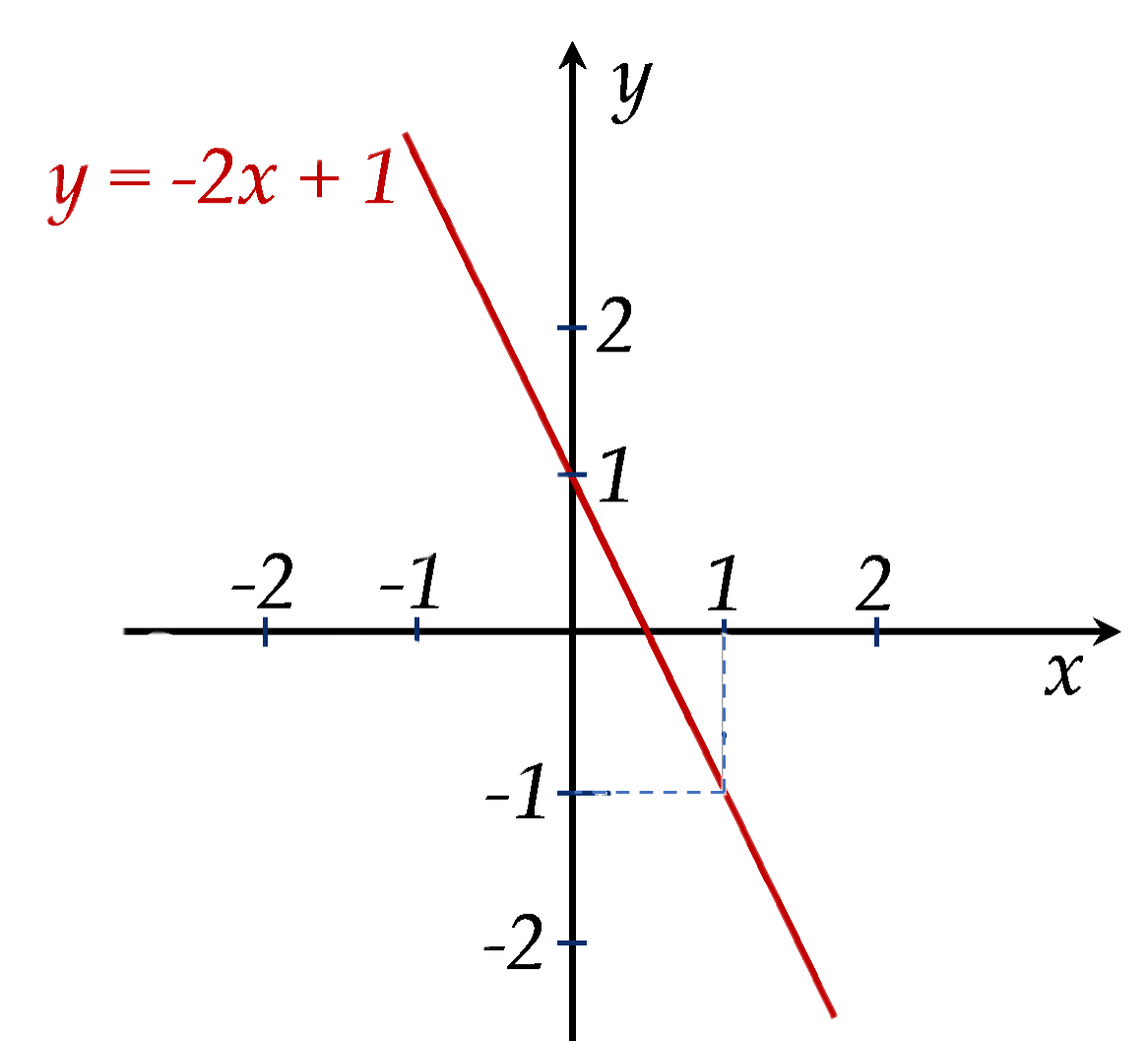
2) Với $ m=0$ ta có hàm số $ y=-2x+1$
Xác định được hai điểm thuộc đồ thị hàm số $ A\left( 1;-1 \right); \, B\left( 0;1 \right)$.
Vẽ đúng đồ thị
3) Ta có: $ \left( d \right)$ // $\left( {{d}'} \right)\Leftrightarrow \left\{ \begin{aligned} & m-2=-3 \\ & m+1\ne 1 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & m=-1 \\ & m\ne 0 \\ \end{aligned} \right.\Leftrightarrow m=-1$ (tmđk)
Vậy $ m=-1$.
Bài 3 (3 điểm)
1) Cho đường tròn $(O)$ và một điểm $P$ nằm ngoài đường tròn $(O)$. Từ $P$ vẽ hai tiếp tuyến $PA$, $PB$ của đường tròn $(O)$ ($A$ và $B$ là hai tiếp điểm tiếp điểm). Gọi $H$ là giao điểm của $OP$ và $AB$.
a) Chứng minh $OP$ vuông góc với $AB$ tại $H$.
b) Từ $A$ vẽ đường kính $AD$ của $(O)$, đường thẳng $PD$ cắt $(O)$ tại $E$ (khác $D$). Chứng minh: $PD.PE = PH.PO$.
2) Chiều rộng của sân bóng đá và của khung thành là $AB = 64,32$ m, $KT = 7,32$ m và $AK = TB$.
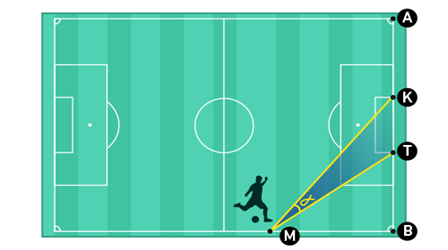
Một cầu thủ điều khiển bóng tấn công dọc theo đường biên và sút bóng tại vị trí $M$ cách $B$ một khoảng $35$ m. Tính góc sút $\alpha $ khi bóng đi trúng khung thành $KT$ (làm tròn đến độ).
Hướng dẫn giải:
1a)
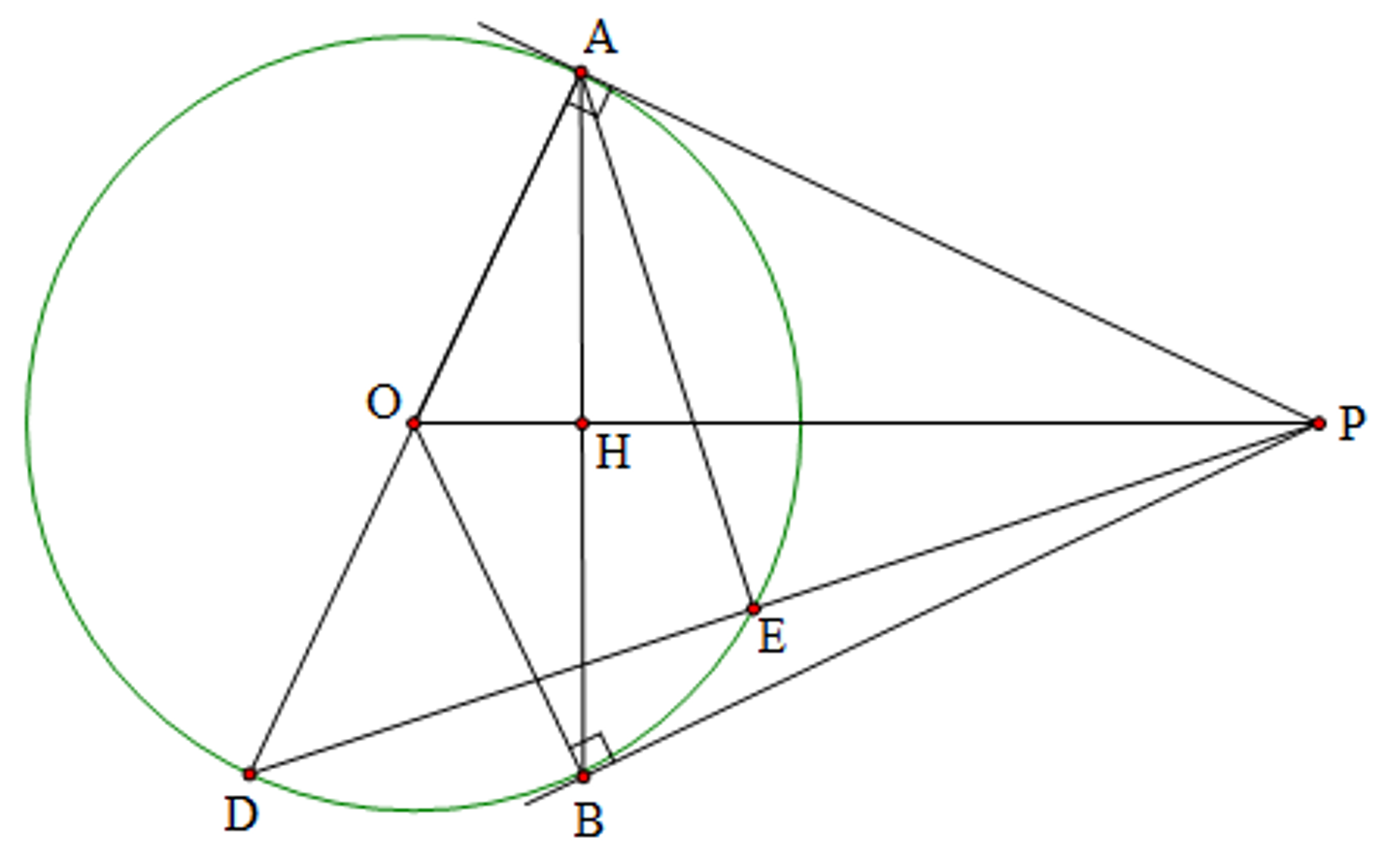
Vì $PA$ và $PB$ là 2 tiếp tuyến của $(O)$ tại $A$ và $B \Rightarrow PA=PB$ (tính chất hai tiếp tuyến cắt nhau)
$\Rightarrow P$ thuộc đường trung trực của $AB$ (1)
Mặt khác ta có $OA = OB = R \Rightarrow O$ thuộc đường trung trực của $AB$ (2)
Từ (1) và (2) $\Rightarrow OP$ là đường trung trực của $AB\Rightarrow PO\bot AB$ tại $H$.
1b) Ta có $ \Delta AED$ nội tiếp đường tròn $(O)$ đường kính $AD \Rightarrow \Delta AED$ vuông tại $E \Rightarrow AE\bot PD$ tại $E$.
Vì $AB$ là tiếp tuyến của $(O)$ nên $AB \perp OB$ suy ra $\Delta ABO$ vuông tại $B$.
Áp dụng hệ thức lượng cho tam giác vuông $PAO$ có: $ PH.PO=P{{A}^{2}}$ (1)
Áp dụng hệ thức lượng cho tam giác vuông $ABD$ có: $ PD.PE=P{{A}^{2}}$ (2)
Từ (1) và (2) $\Rightarrow PH.PO=PD.PE$
2)
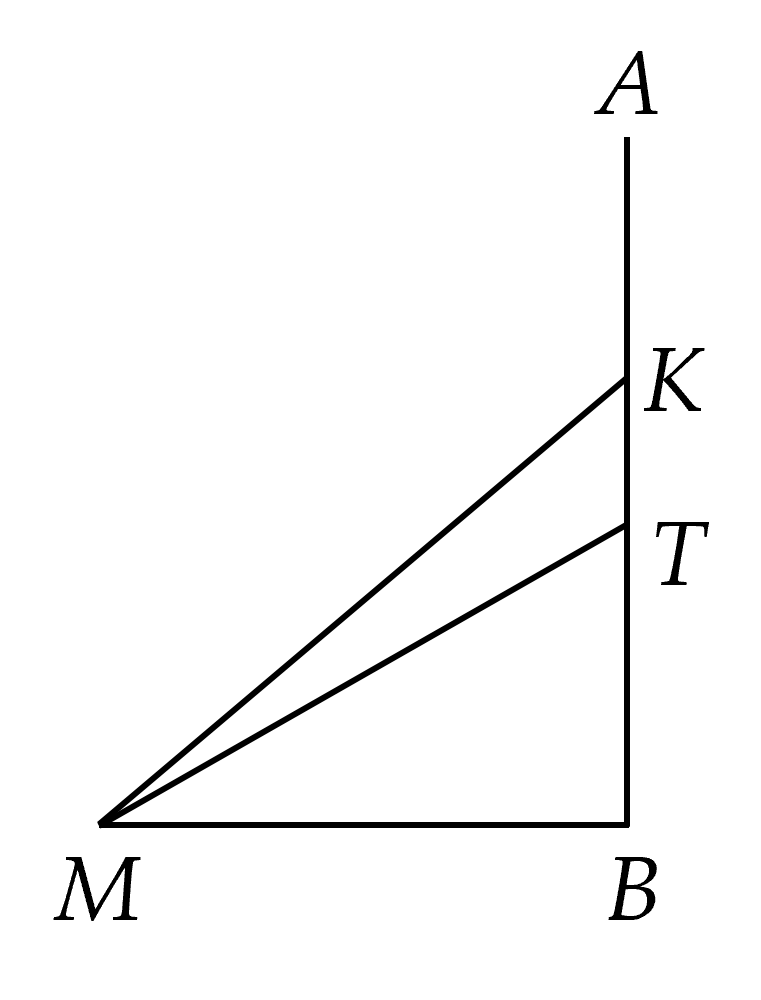
Xét $\Delta MBK$ vuông tại $B$ có $\tan \widehat{KMB}=\dfrac{KB}{MB}=\dfrac{35,82}{35}\Rightarrow \widehat{KMB}\approx {{46}^{\circ}}$
Xét $\Delta MBT$ vuông tại $B$ có $\tan \widehat{TMB}=\dfrac{TB}{MB}=\dfrac{28,5}{35}\Rightarrow \widehat{TMB}\approx {{39}^{\circ}}$.
Tính được góc sút $\alpha =\widehat{KMT}\approx {{7}^{\circ}}$.
Bài 4 (1 điểm). Giải phương trình $(x+5)\sqrt{2x+3}=-4{{x}^{2}}+2x+54.$
Hướng dẫn giải:
$(x+5)\sqrt{2x+3}=-4{{x}^{2}}+2x+54$ (1)
ĐK: $x\ge -\dfrac{3}{2}$
(1) $\Leftrightarrow (x+5)\sqrt{2x+3}-3(x+5)=-4{{x}^{2}}-x+39 $
$\Leftrightarrow (x+5)(\sqrt{2x+3}-3)=-4{{x}^{2}}-x+39$
$ \Leftrightarrow \dfrac{2(x+5)(x-3)}{\sqrt{2x+3}+3}+(x-3)(4x+13)=0$
$\Leftrightarrow (x-3)\left( \dfrac{2x+10}{\sqrt{2x+3}+3}+4x+13 \right)=0$
$\Leftrightarrow x-3=0$ (vì $\dfrac{2x+10}{\sqrt{2x+3}+3}+4x+13>0, \, \forall x\ge -\dfrac{3}{2}$)
$\Leftrightarrow x=3$ (Thoả mãn).
Vậy phương trình có nghiệm duy nhất $x=3$.
