Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) Tổng số học sinh của lớp là: 40.

Số học sinh Tốt chiếm số phần trăm là:

     16 : 40 . 100% = 40%

Số học sinh Khá chiếm số phần trăm là:

     11 : 40 . 100% = 27,5%

b) Số học sinh xếp loại Chưa đạt chiếm số phần trăm là:

     3 : 40 . 100% = 7,5%

Cô giáo thông báo tỉ lệ học sinh xếp loại Chưa đạt của lớp chiếm trên 7% là đúng.

Hướng dẫn giải:

a) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm" là $\dfrac{22}{40} =  \dfrac{11}{20}$.

b) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 6 chấm" là $\dfrac{18}{40} =  \dfrac{9}{20}$.

c) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 1 chấm" là $\dfrac{14}{40} =  \dfrac{7}{20}$.

d) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 3 chấm" là $\dfrac{14}{20} =  \dfrac{7}{10}$.

Hướng dẫn giải:

a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

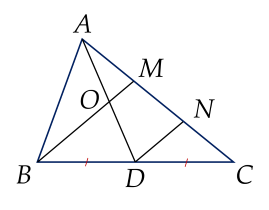
Xét $\Delta MBC$ có $DB = DC$ và $DN$ // $BM$ nên $MN=NC=\dfrac{1}{2} MC$ (định lí đường trung bình của tam giác).

Mặt khác $AM=\dfrac{1}{2} MC$, do đó $AM=MN=\dfrac{1}{2} MC$.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên $OM=\dfrac{1}{2} DN$ (1) 

Xét $\Delta MBC$ có $DN$ là đường trung bình nên $DN=\dfrac{1}{2} BM$. (2)

Từ (1) và (2) ta có $OM=\dfrac{1}{4} BM$.

Hướng dẫn giải:

$D(x)=2\left(x^2-x\right)+\left(3 y^2-2 y\right)+\left(4 z^2-2 z\right)+2$

$=2\left(x^2-x+\dfrac{1}{4}\right)+3\left(y^2-\frac{2}{3} y+\dfrac{1}{9}\right)+\left[(2 z)^2-2 z+\dfrac{1}{4}\right]+2-\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{4}$

$=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+\left(2 z-\dfrac{1}{2}\right)^2+\dfrac{11}{2} \geq \dfrac{11}{2}$

Vậy giá trị nhỏ nhất của $D$ là: $\dfrac{11}{2}$ tại $(x, y, z)=\left(\dfrac{1}{2} ; \dfrac{1}{3} ; \dfrac{1}{4}\right)$.