Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

(Lý thuyết) Bài 8. Các góc ở vị trí đặc biệt. Tia phân giác của một góc. SVIP
1. Các góc ở vị trí đặc biệt
a. Hai góc kề bù
Định nghĩa:
Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

Tính chất của hai góc kề bù
Hai góc kề bù có tổng số đo bằng $180^\circ$.
Chú ý
1. Hai góc kề bù còn được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó:
- Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó. Chẳng hạn, trong hình dưới, góc $xOy$ và góc $yOz$ là hai góc kề nhau.

- Hai góc bù nhau là hai góc có tổng số đo bằng $180^\circ$.
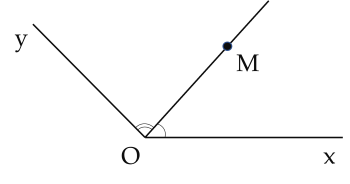
2. Nếu điểm $M$ nằm trong góc $xOy$ thì ta nói $OM$ nằm giữa hai cạnh (hai tia) $Ox$ và $Oy$ của góc $xOy$. Khi đó ta có:
b. Hai góc đối đỉnh
Định nghĩa
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia.

Tính chất của hai góc đối đỉnh
Hai góc đối đỉnh thì bằng nhau.
Ví dụ 1: Cho hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$. Biết $\widehat{xOy}=60^\circ$. Tính số đo các góc $x'Oy'$ và $x'Oy$.
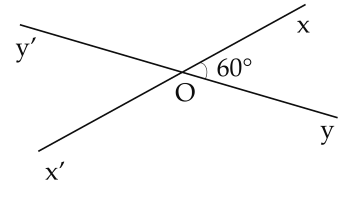
Giải
Ta có:
$\widehat{x'Oy'} = \widehat{xOy}$ (hai góc đối đỉnh).
Suy ra $\widehat{x'Oy'} = 60^\circ$.
$\widehat{x'Oy} + \widehat{xOy} = 180^\circ$.
Suy ra:
$\widehat{x'Oy} = 180^\circ - \widehat{xOy} $
$\widehat{x'Oy} = 180^\circ - 60^\circ $
$\widehat{x'Oy} = 120^\circ$
2. Tia phân giác của một góc
Định nghĩa
Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
Tính chất của tia phân giác
Khi $Oz$ là tia phân giác của góc $xOy$ thì $\displaystyle\widehat{xOz}=\widehat{yOz}=\frac{1}{2}\widehat{xOy}$.
Lưu ý: Đường thẳng chứa tia phân giác của một góc gọi là đường phân giác của góc đó.

Ví dụ 2: Cho $\widehat{mOn}$ = $70^\circ$, tia $Ot$ là tia phân giác của $\widehat{mOn}$. Tính số đo hai góc $mOt$ và $tOn$.

Giải
Vì $Ot$ là tia phân giác góc $mOn$ nên
$\widehat{mOt}=\widehat{tOn}=\displaystyle\frac{1}{2}\widehat{mOn}=\frac{1}{2}.70^\circ=35^\circ$
Bạn có thể đăng câu hỏi về bài học này ở đây


