Lý thuyết SVIP

1. Góc giữa hai vectơ

Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác \(\overrightarrow{0}\). Từ một điểm \(O\) bất kì ta vẽ \(\overrightarrow{OA}=\overrightarrow{a}\), \(\overrightarrow{OB}=\overrightarrow{b}\). Góc \(\widehat{AOB}\) với số đo từ \(0^o\) đến \(180^o\) được gọi là góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). 

Ta kí hiệu góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là \(\left(\overrightarrow{a},\overrightarrow{b}\right)\). 

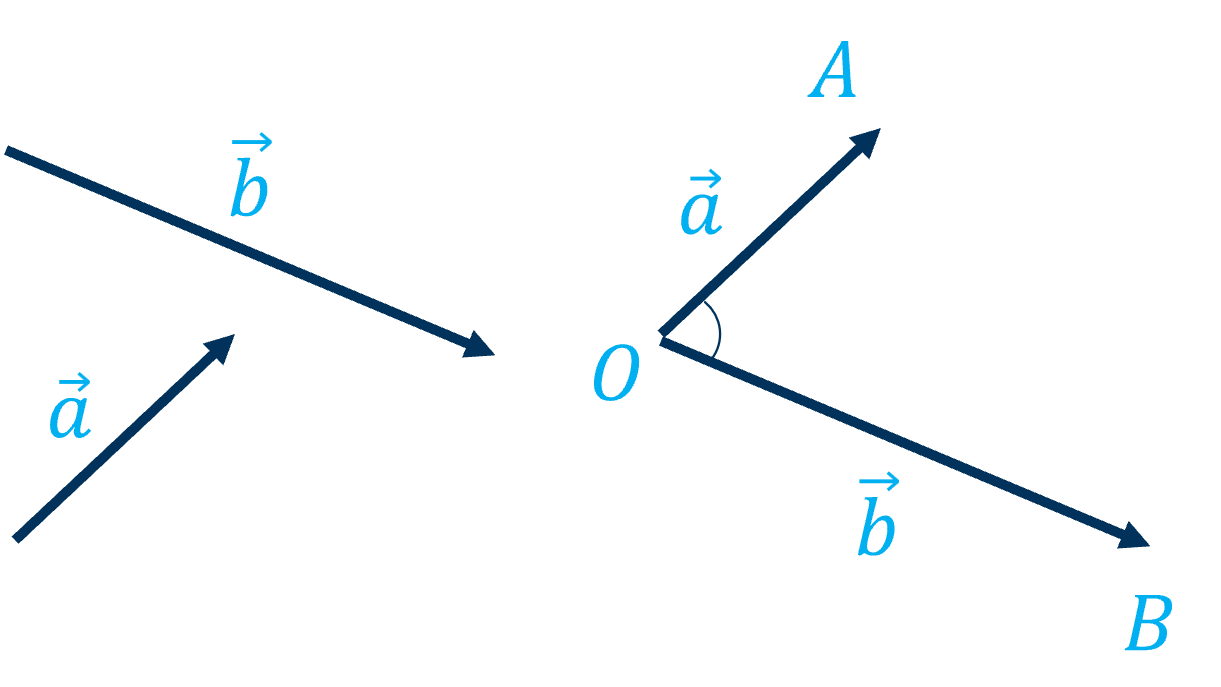
Nếu \(\left(\overrightarrow{a},\overrightarrow{b}\right)=90^o\) thì ta nói rằng \(\overrightarrow{a}\) và \(\overrightarrow{b}\) vuông góc với nhau, kí hiệu là \(\overrightarrow{a}\perp\overrightarrow{b}\). 

Chú ý

- Từ định nghĩa ta có \(\left(\overrightarrow{a},\overrightarrow{b}\right)=\left(\overrightarrow{b},\overrightarrow{a}\right)\).

- Góc giữa hai vectơ cùng hướng và khác \(\overrightarrow{0}\) luôn bằng \(0^o\).

- Góc giữa hai vectơ ngược hướng và khác \(\overrightarrow{0}\) luôn bằng \(180^o\).

- Trong trường hợp có ít nhất một trong hai vectơ \(\overrightarrow{a}\) hoặc \(\overrightarrow{b}\) là vectơ \(\overrightarrow{0}\) thì ta quy ước số đo góc giữa hai vectơ đó là tùy ý (từ \(0^o\) đến \(180^o\)).

Ví dụ 1: Cho hình vuông \(ABCD\) có tâm \(I\). Tìm các góc: 

a) \(\left(\overrightarrow{DC},\overrightarrow{AB}\right)\); \(\left(\overrightarrow{CD},\overrightarrow{AB}\right)\);

b) \(\left(\overrightarrow{AB},\overrightarrow{BC}\right)\). 

Giải

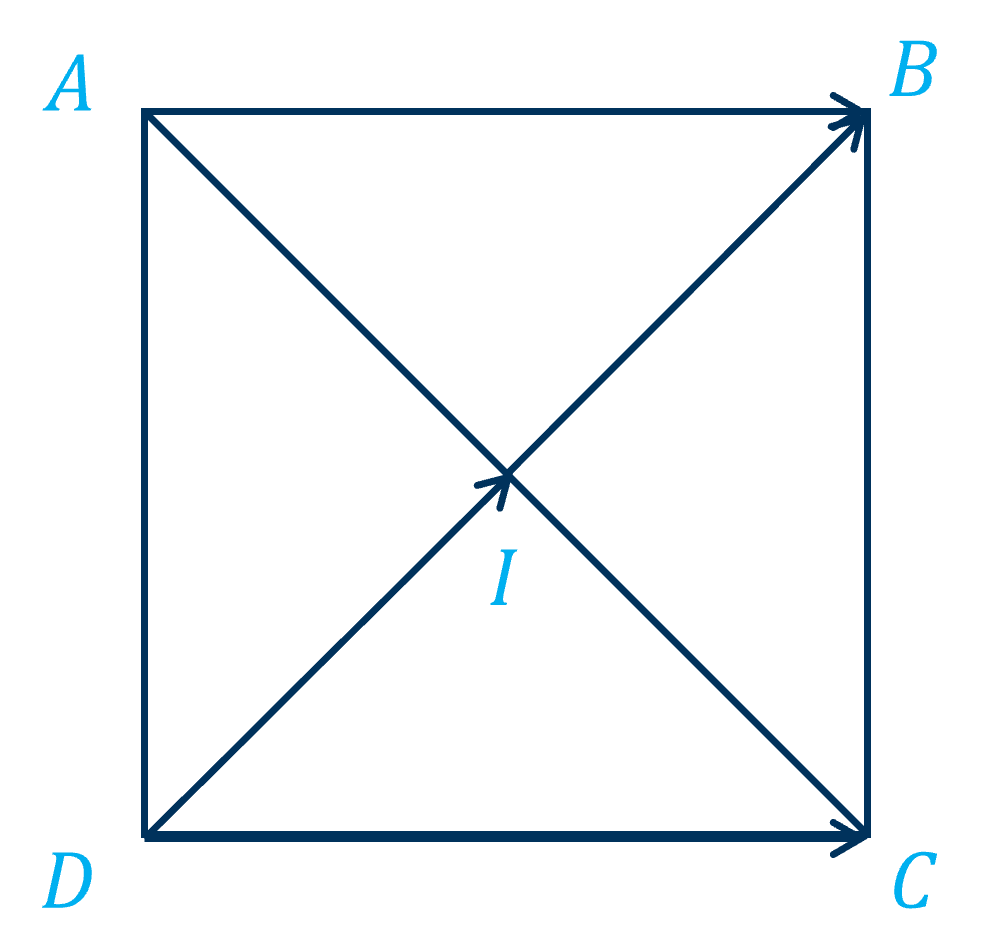
a) Do hai vectơ \(\overrightarrow{DC}\), \(\overrightarrow{AB}\) cùng hướng nên \(\left(\overrightarrow{DC},\overrightarrow{AB}\right)=0^o\).

Do hai vectơ \(\overrightarrow{CD}\), \(\overrightarrow{AB}\) ngược hướng nên \(\left(\overrightarrow{CD},\overrightarrow{AB}\right)=180^o\).

b) Do hai vectơ \(\overrightarrow{AB}\), \(\overrightarrow{BC}\) vuông góc nên \(\left(\overrightarrow{AB},\overrightarrow{BC}\right)=90^o\).

2. Tích vô hướng của hai vectơ

Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác \(\overrightarrow{0}\).

Tích vô hướng của \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là một số, kí hiệu là \(\overrightarrow{a}.\overrightarrow{b}\), được xác định bởi công thức:

\(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos\left(\overrightarrow{a},\overrightarrow{b}\right)\).

Chú ý

- Trường hợp ít nhất một trong hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) bằng \(\overrightarrow{0}\), ta quy ước \(\overrightarrow{a}.\overrightarrow{b}=0\).

- Với hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác \(\overrightarrow{0}\), ta có \(\overrightarrow{a}\perp\overrightarrow{b}\Leftrightarrow\overrightarrow{a}.\overrightarrow{b}=0\).

Ta có \(\overrightarrow{a}^2=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}\right|.\cos0^o=\left|\overrightarrow{a}\right|^2\). Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó. 

Ví dụ 2: Cho tam giác \(ABC\) vuông cân tại \(A\), có cạnh \(BC\) bằng \(\sqrt{2}\). Tính các tích vô hướng: \(\overrightarrow{AB}.\overrightarrow{AC}\); \(\overrightarrow{AC}.\overrightarrow{BC}\); \(\overrightarrow{AB}.\overrightarrow{BC}\).

Giải

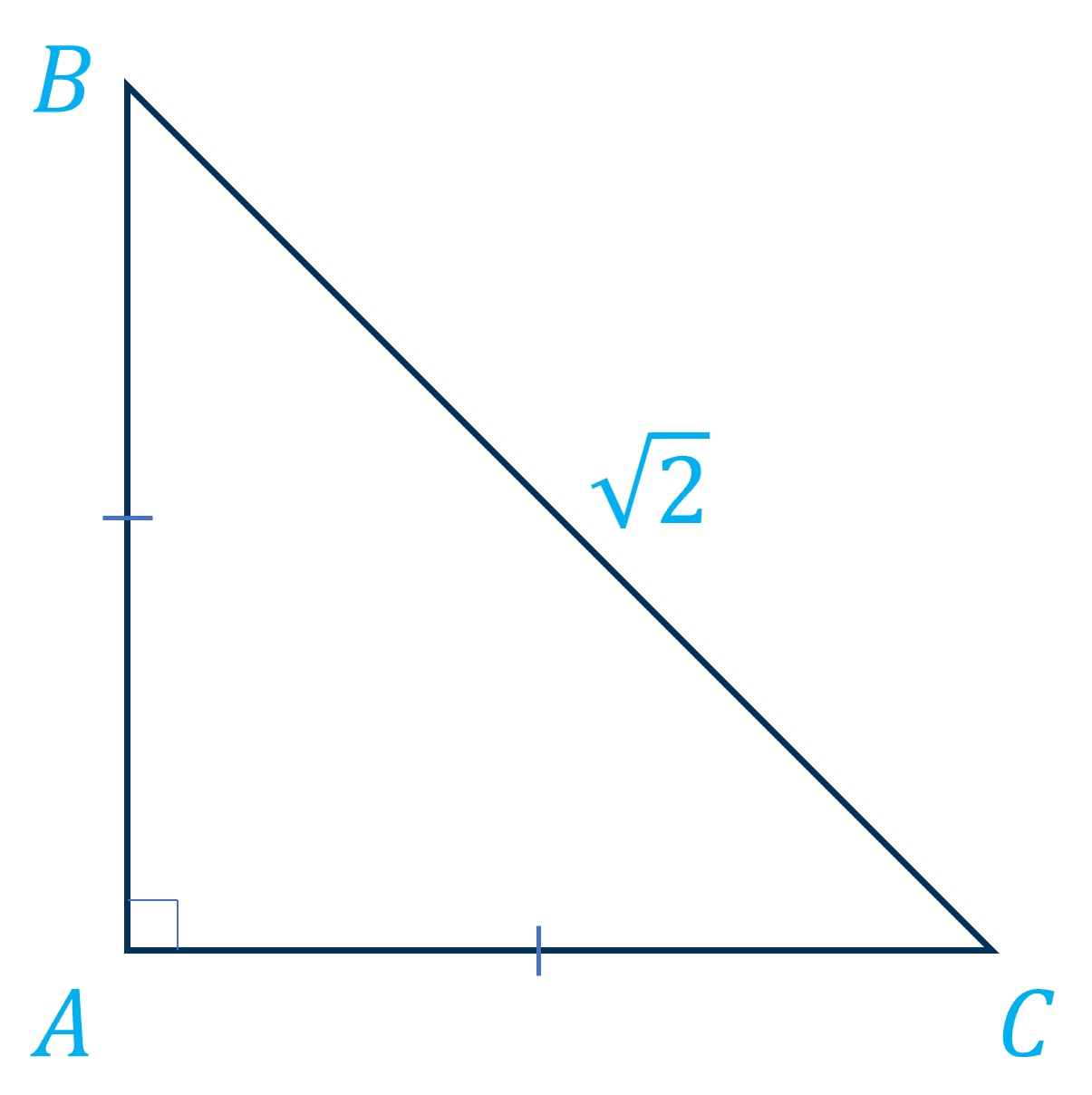
Tam giác \(ABC\) vuông cân tại \(A\) có \(BC=\sqrt{2}\) suy ra \(AB=AC=1\).

\(\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.\cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=1.1.\cos90^o=0\).

\(\overrightarrow{AC}.\overrightarrow{BC}=\left|\overrightarrow{AC}\right|.\left|\overrightarrow{BC}\right|.\cos\left(\overrightarrow{AC},\overrightarrow{BC}\right)=1.\sqrt{2}.\cos45^o=\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\).

\(\overrightarrow{AB}.\overrightarrow{BC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{BC}\right|.\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)=1.\sqrt{2}.\cos135^o=\sqrt{2}.\left(-\dfrac{\sqrt{2}}{2}\right)=-1\).

3. Tính chất của tích vô hướng

Với ba vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\) bất kì và mọi số \(k\), ta có: 

• \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}\);
• \(\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}\);
• \(\left(k\overrightarrow{a}\right).\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)\).

- Từ các tính chất của tích vô hướng của hai vectơ, ta suy ra: 

• \(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\overrightarrow{a}^2+2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\);
• \(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\);
• \(\left(\overrightarrow{a}+\overrightarrow{b}\right).\left(\overrightarrow{a}-\overrightarrow{b}\right)=\overrightarrow{a}^2-\overrightarrow{b}^2\).

Ví dụ 3: Cho hai vectơ \(\overrightarrow{i}\), \(\overrightarrow{j}\) vuông góc có cùng độ dài bằng \(1\) và cho biết \(\overrightarrow{a}=4\overrightarrow{i}-\overrightarrow{j}\), \(\overrightarrow{b}=\overrightarrow{i}+4\overrightarrow{j}\). Tính tích vô hướng \(\overrightarrow{a}.\overrightarrow{b}\) và tính số đo góc \(\left(\overrightarrow{a},\overrightarrow{b}\right)\).

Giải

Ta có \(\overrightarrow{a}.\overrightarrow{b}=\left(4\overrightarrow{i}-\overrightarrow{j}\right)\left(\overrightarrow{i}+4\overrightarrow{j}\right)=4\overrightarrow{i}^2+16\overrightarrow{i}.\overrightarrow{j}-\overrightarrow{j}.\overrightarrow{i}-4\overrightarrow{j}^2=4-4=0\).

Vậy \(\overrightarrow{a}.\overrightarrow{b}=0\) do đó \(\left(\overrightarrow{a},\overrightarrow{b}\right)=90^o\).

4. Áp dụng của tích vô hướng

Trong Vật lí, tích vô hướng giúp tính công \(A\) sinh bởi một lực \(\overrightarrow{F}\) có độ dịch chuyển là vectơ \(\overrightarrow{d}\). Ta có công thức: \(A=\overrightarrow{F}.\overrightarrow{d}\).

Ví dụ 4: Tính công sinh bởi một lực \(\overrightarrow{F}\) có độ lớn \(20\) \(N\) kéo một vật dịch chuyển theo một vectơ \(\overrightarrow{d}\) có độ dài \(50m\) và cho biết \(\left(\overrightarrow{F},\overrightarrow{d}\right)=60^o\).

Giải

Ta có \(A=\overrightarrow{F}.\overrightarrow{d}=\left|\overrightarrow{F}\right|.\left|\overrightarrow{d}\right|.\cos\left(\overrightarrow{F},\overrightarrow{d}\right)=20.50.\cos60^o=20.50.\dfrac{1}{2}=500\left(J\right)\).