Bài học cùng chủ đề
- Giá trị lượng giác của một góc từ 0° đến 180°
- Quan hệ giữa các giá trị lượng giác của 2 góc bù nhau
- So sánh các GTLG. Tính giá trị biểu thức lượng giác
- Giá trị lượng giác của góc 0 độ đến 180 độ
- Quan hệ của GTLG của hai góc bù nhau, phụ nhau
- Luyện tập tổng hợp
- Bài tập tự luận (nâng cao)
- Phiếu bài tập: Giá trị lượng giác của một góc
- Giá trị lượng giác của một góc từ $0^\circ$ độ đến $180^\circ$
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Giá trị lượng giác của một góc từ $0^\circ$ độ đến $180^\circ$ SVIP
Nội dung này do giáo viên tự biên soạn.
1. GIÁ TRỊ LƯỢNG GIÁC
Trong mặt phẳng tọa độ \(Oxy\), nửa đường tròn tâm \(O\), bán kính \(R=1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
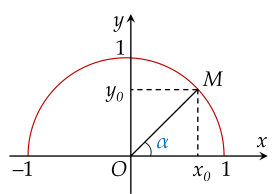
Với mỗi góc \(\alpha\), \(0^\circ\leq \alpha\leq 180^\circ\), ta xác định duy nhất một điểm \(M\left(x_0;y_0\right)\) trên nửa đường tròn đơn vị sao cho \(\widehat{xOM}=\alpha\). Khi đó:
- Tung độ \(y_0\) của \(M\) là \(\sin\) của góc \(\alpha\), kí hiệu là \(\sin\alpha=y_0;\)
- Hoành độ \(x_0\) của \(M\) là côsin của góc \(\alpha\), kí hiệu là \(\cos\alpha=x_0;\)
- Tỉ số \(\dfrac{y_0}{x_0}\left(x_0\ne0\right)\) là tang của góc \(\alpha\), kí hiệu là \(tan\alpha=\dfrac{y_0}{x_0}\);
- Tỉ số \(\dfrac{x_0}{y_0}\left(y_0\ne0\right)\) là côtang của góc \(\alpha\), kí hiệu là \(\cot\alpha=\dfrac{x_0}{y_0}\).
Các số \(\sin\alpha,\cos\alpha,\tan\alpha,\cot\alpha\) được gọi là giá trị lượng giác của góc \(\alpha\).
Chú ý:
a) Nếu \(\alpha\) là góc nhọn thì các giá trị lượng giác của \(\alpha\) đều dương.
Nếu \(\alpha\) là góc tù thì \(\sin\alpha>0,\cos\alpha< 0,\tan\alpha< 0,\cot\alpha< 0.\)
b) \(\tan\alpha\) chỉ xác định khi \(\alpha\ne90^\circ\).
\(\cot\alpha\) chỉ xác định khi \(\alpha\ne0^\circ,\alpha\ne180^\circ.\)
2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Với mọi góc \(\alpha\) thỏa mãn \(0^\circ\le\alpha\le180^\circ\) thì:
\(\sin \left (180^\circ-\alpha\right )=\sin\alpha \),
\(\cos \left (180^\circ-\alpha\right )=-\cos\alpha \),
\(\tan \left (180^\circ-\alpha\right )=-\tan\alpha \left ( \alpha \neq 90^\circ \right )\),
\(\cot \left (180^\circ-\alpha\right )=-\cot\alpha\left ( 0^\circ< \alpha < 180^\circ \right )\).
3. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT
Bảng giá trị lượng giác của một số góc đặc biệt
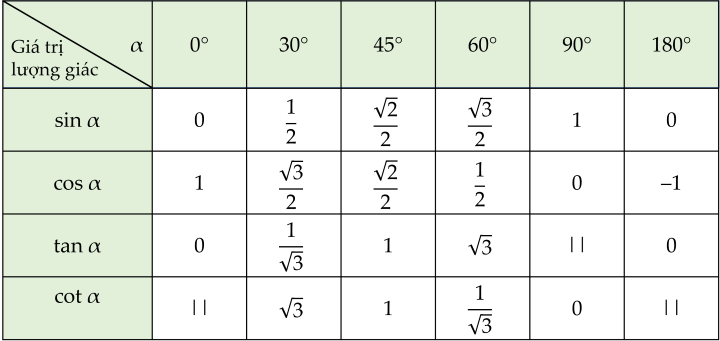
Ví dụ.
\(\sin150^\circ=\sin\left ( 180^\circ-30^\circ \right )=\sin30^\circ=\frac{1}{2}\);
\(\tan120^\circ=\tan\left (180^\circ-60^\circ\right )=-\tan60^\circ=-\sqrt{3}\).

Bạn có thể đánh giá bài học này ở đây