Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Đồ thị và sự biến thiên của hàm số lượng giác SVIP
Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với OLM
Câu 1 (1đ):
Hàm số y=cosx đồng biến trên khoảng nào sau đây?
(0;π).
(−π;0).
(2−π;2π).
(2π;π).
Câu 2 (1đ):
Hàm số y=cosx nghịch biến trên khoảng nào dưới đây?
(−π;−2π).
(−2π;0).
(0;π).
(−2π;2π).
Câu 3 (1đ):
Hàm số y=sinx đồng biến trên khoảng nào dưới đây?
(π;2π).
(2π;π).
(23π;2π).
(2π;23π).
Câu 4 (1đ):
Hai hàm số nào sau đây tăng trên khoảng (0;2π)?
y=tanx và y=cotx.
y=cotx và y=sinx.
y=sinx và y=tanx.
y=sinx và y=cosx.
Câu 5 (1đ):
Xét hàm số y=sinx trên đoạn [−π;0]. Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên các khoảng (−π;−2π) và (−2π;0).
Hàm số nghịch biến trên khoảng (−π;−2π); đồng biến trên khoảng (−2π;0).
Hàm số đồng biến trên các khoảng (−π;−2π) và (−2π;0).
Hàm số đồng biến trên khoảng (−π;−2π); nghịch biến trên khoảng (−2π;0).
Câu 6 (1đ):
Trên khoảng (−6π;−5π), hàm số nào sau đây luôn nhận giá trị dương?
y=tanx
y=cosx.
y=cotx.
y=sinx.
Câu 7 (1đ):
Xét hàm số y=cosx trên khoảng (5π;34π). Hàm số đồng biến trên khoảng có độ dài là
6π.
4π.
127π.
3π.
Câu 8 (1đ):
Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?
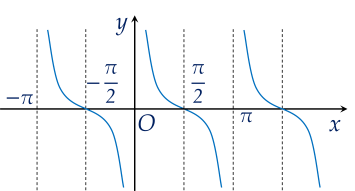
y=cotx.
y=tanx.
y=cosx.
y=sinx.
Câu 9 (1đ):
Đường cong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số sau?
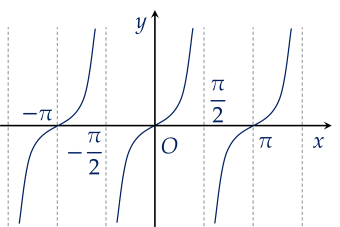
y=cosx.
y=cotx.
y=tanx.
y=sinx.
Câu 10 (1đ):
Cho các hàm số f(x)=sinx và g(x)=cosx.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số f(x)=sinx đồng biến trên khoảng (−2π;2π). |
|
| b) Hàm số f(x) nghịch biến trên khoảng (43π;45π). |
|
| c) Hàm số g(x) nghịch biến trên khoảng (0;π). |
|
| d) Hàm số g(x) đồng biến trên khoảng (625π;313π). |
|
25%
Đúng rồi !

Hôm nay, bạn còn lượt làm bài tập miễn phí.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây