Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Bài giảng video tương tác có điểm dừng phần:
Định nghĩa hai tam giác đồng dạng.
Qua bài học này người học sẽ nắm được:
- Định nghĩa hai tam giác đồng dạng.
- Cách kiểm tra và chứng minh hai tam giác đồng dạng.
- Trình bày cách chứng minh và kiểm tra hai tam giác đồng dạng.
Kéo thả phương án đúng vào ô trống.
A= .
B= .
C= .
(Kéo thả hoặc click vào để điền)
Điền số thích hợp vào ô trống.
| AB | = | |
| DE |
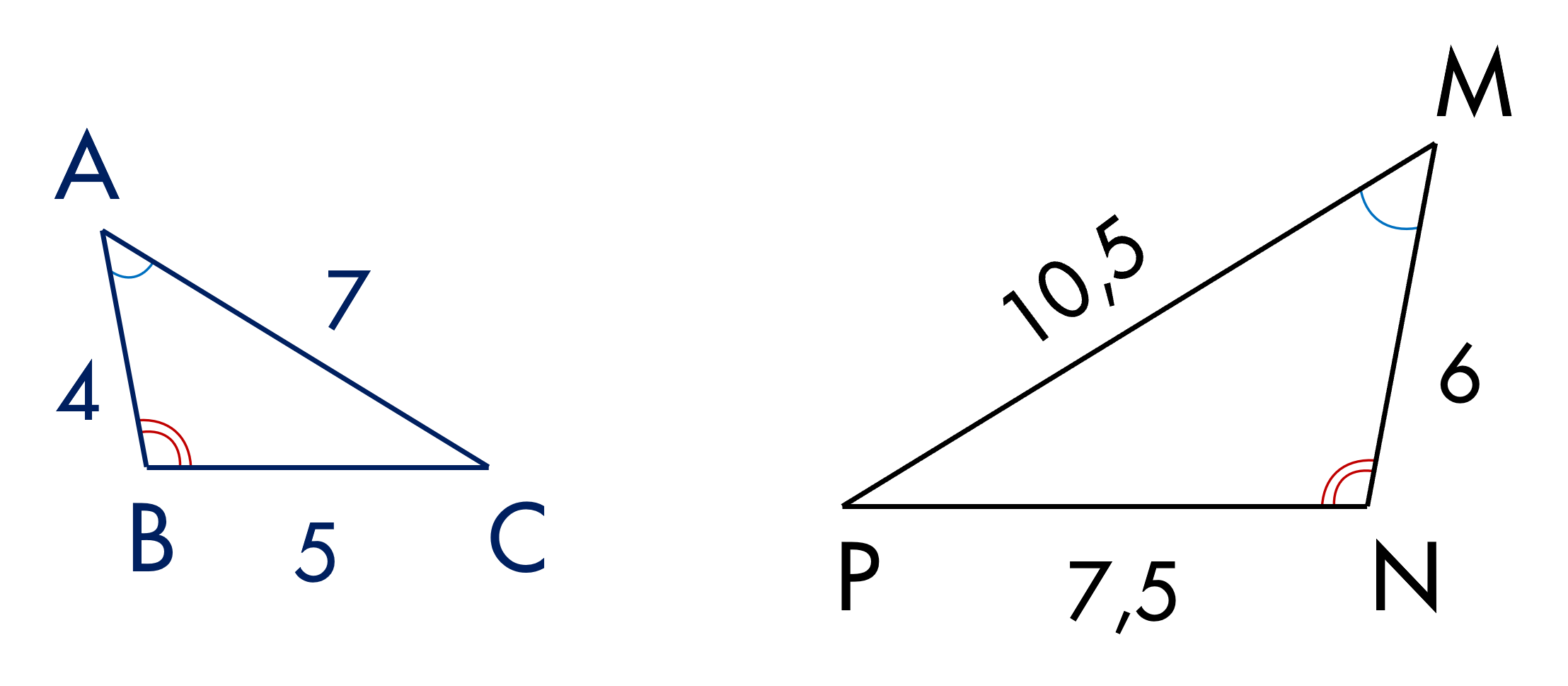
Kéo thả các góc tương ứng vào ô trống.
A= .
B= .
C= .
(Kéo thả hoặc click vào để điền)
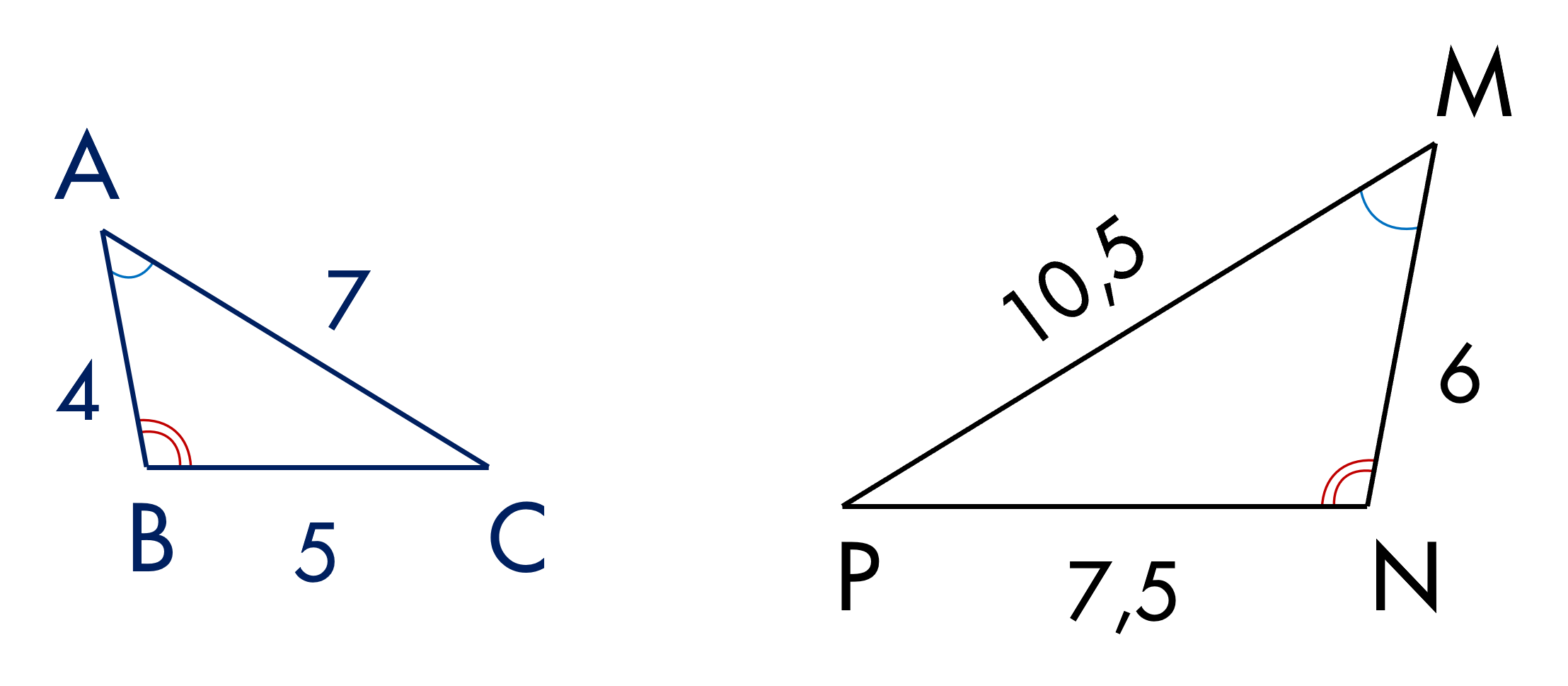
Kéo thả các cạnh tương ứng tỉ lệ vào ô trống.
| AB | = | BC | = | AC |
(Kéo thả hoặc click vào để điền)
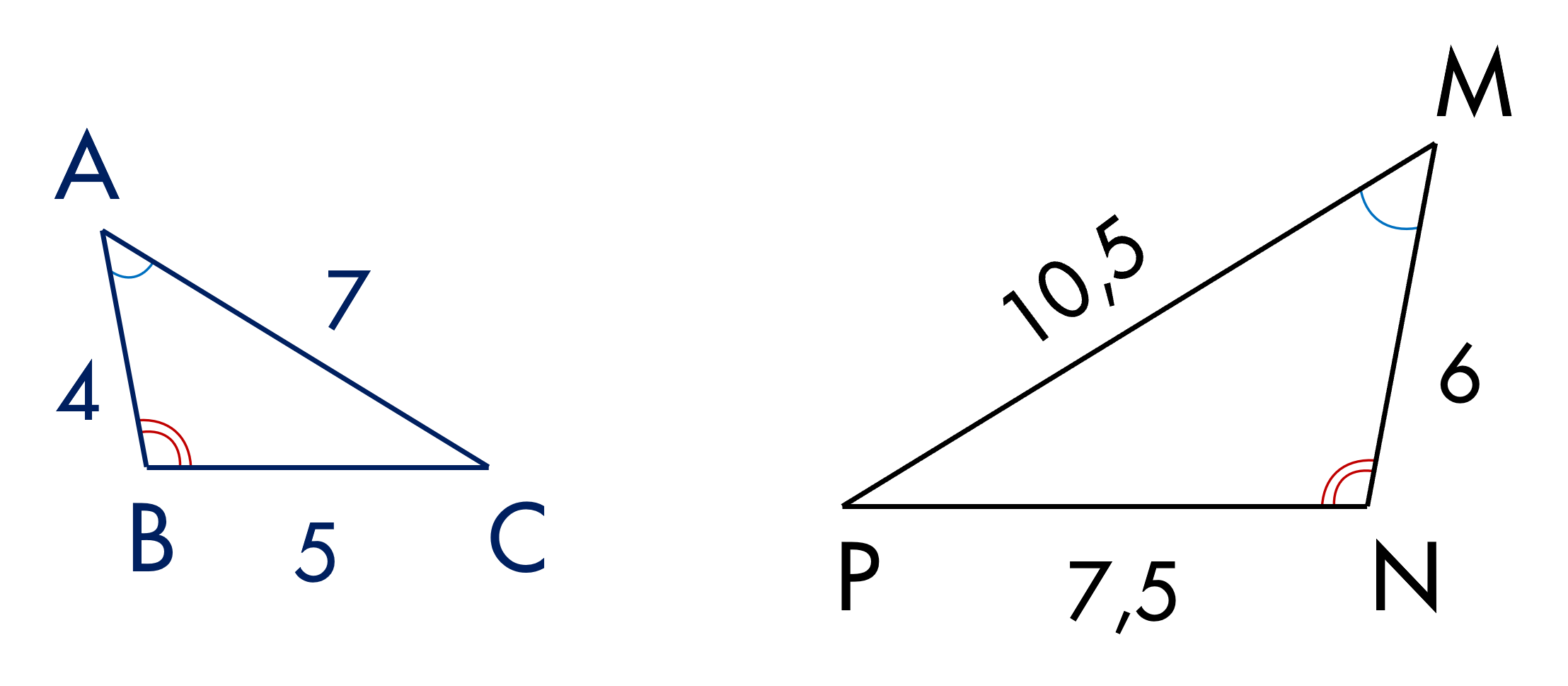
Điền các chữ thích hợp để hoàn thành kí hiệu đồng dạng.
Lưu ý: Khi viết cần đảm bảo đúng các đỉnh tương ứng.
ΔABC∽Δ.
Cho ΔABC∽ΔA′B′C′. Chọn khẳng định sai?
Nếu tam giác ABC đồng dạng với tam giác DEF theo tỉ số m thì tam giác DEF đồng dạng với tam giác ABC theo tỉ số
Chọn khẳng định sai.
Cho ΔABC∽ΔMNP. Tính số đo góc x.
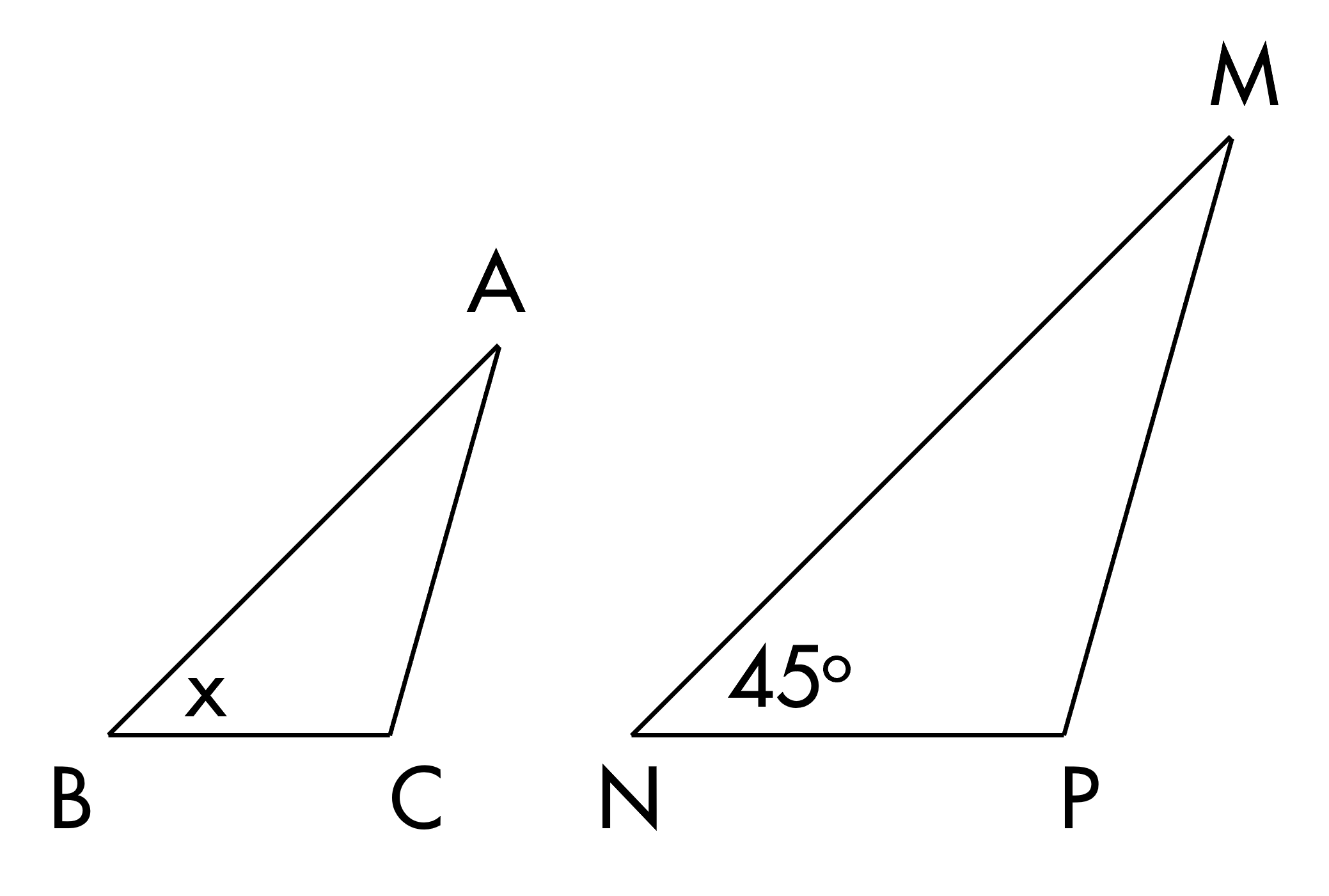
x= ∘.
Cho ΔABC∽ΔMNP. Tính độ dài cạnh BC.
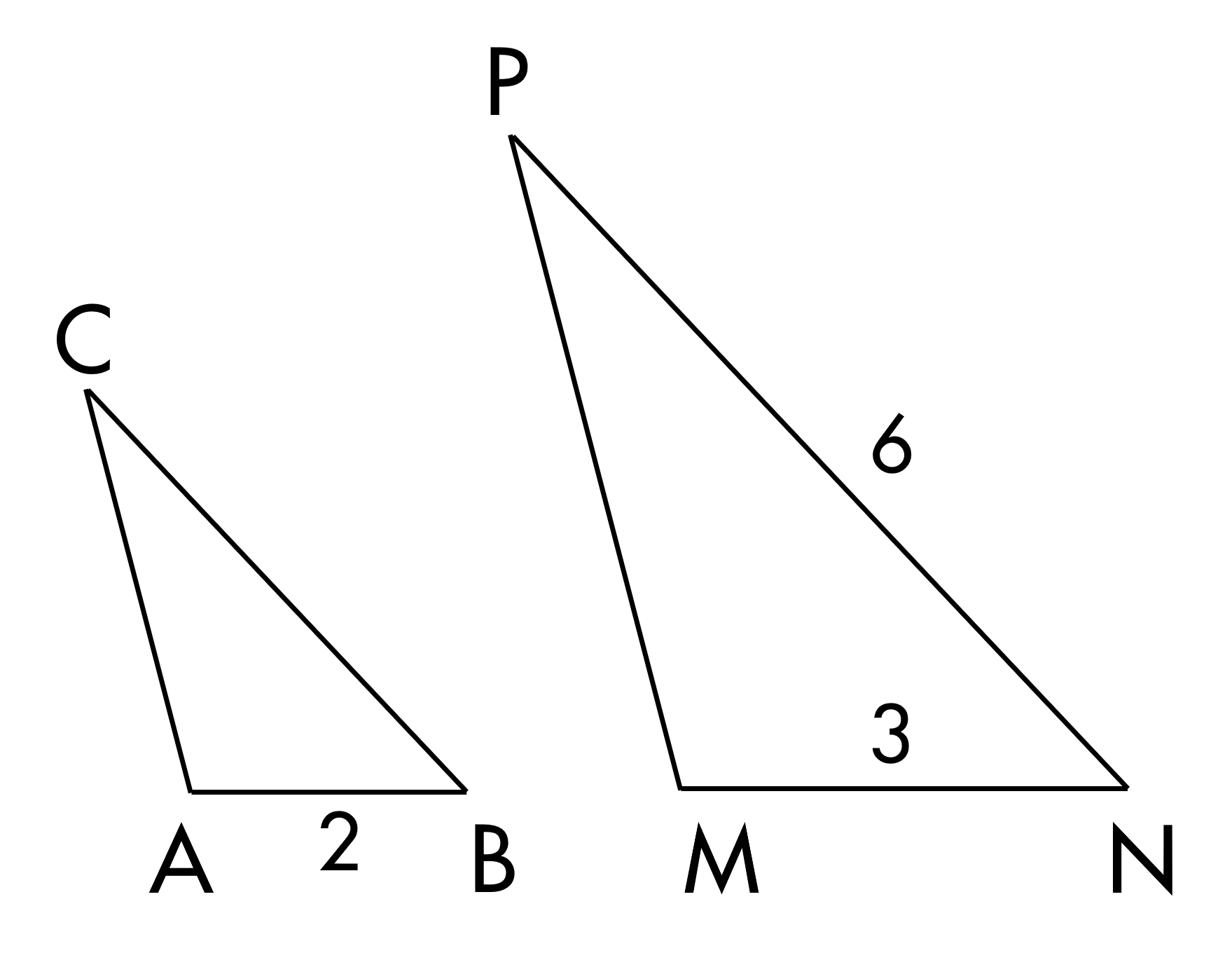
BC= .
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Chào mừng các em đã đến với bài học mới
- trên trang web
- olm.vn và trong bài học lần này chúng ta
- sẽ cùng nhau tìm hiểu về hai tam giác
- đồng
- Dạ nội dung bài học gồm có hai phần phần
- đầu tiên chúng ta sẽ cùng nhau tìm hiểu
- về định nghĩa thế nào là hai tam giác
- đồng
- dạng và phần số hai thì chúng ta sẽ cùng
- nhau tìm hiểu về định lý tam giác đồng
- dạng
- Chúng Ta Đi Vào phần đầu
- tiên chúng ta đã được học hai tam giác
- bằng nhau ở lớp dưới cụ thể khi hai tam
- giác ABC bằng với tam giác
- a'b'c' khi trùng có các cạnh tương ứng
- bằng nhau và các góc tương ứng bằng
- nhau bây giờ thầy sẽ chỉ ra cho các em
- một ví dụ về hai tam giác không bằng
- nhau nhưng giống hình
- dạng ở trên màn hình thì chúng ta có thể
- thấy hai tam giác
- MNP và m'n php' không bằng nhau Tuy
- nhiên chúng lại có hình dạng khá giống
- nhau và cụ thể hơn thì tam giác m'n php'
- trông giống như một phiên bản nhỏ hơn
- của tam giác
- MNP và người ta gọi đây là hai tam giác
- đồng dạng đồng dạng có nghĩa là cùng
- hình dạng bây giờ chúng ta sẽ cùng nhau
- đi vào nội dung chính của phần định
- nghĩa hoạt động đầu
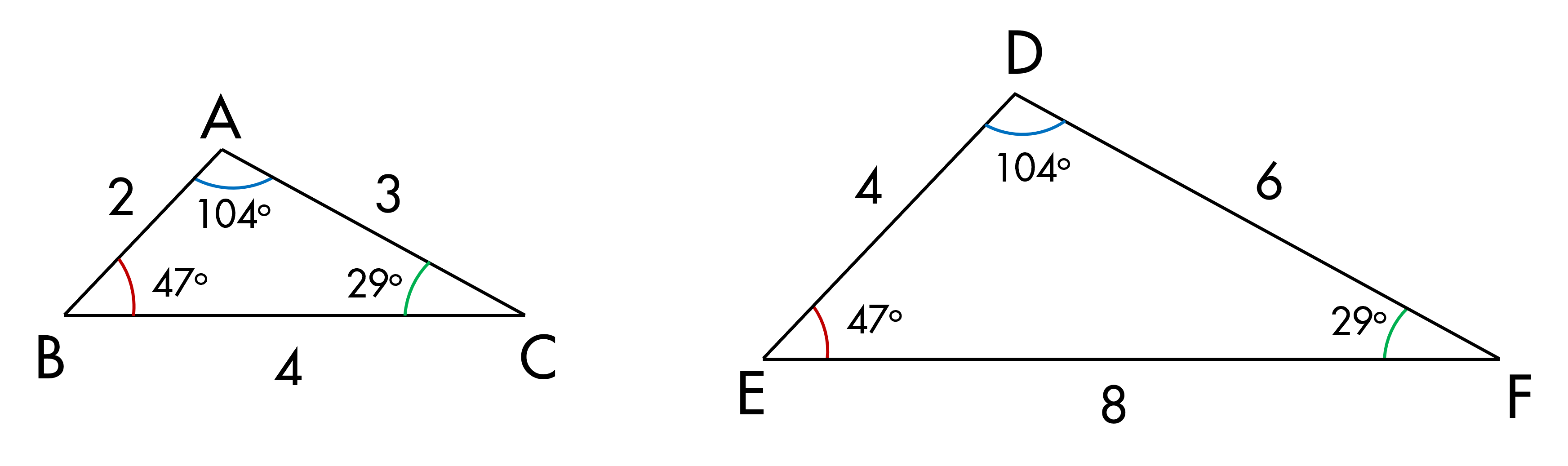
- tiên cho hai tam giác A ABC và tam giác
- df có các kích thước như
- sau Các em có thể thấy kích thước của
- từng cạnh và từng góc của tam giác ở
- trên màn
- hình câu hỏi đầu tiên chỉ ra các CP góc
- bằng nhau ở hai tam
- giác chúng ta có thể thấy góc A bằng với
- góc D cùng bằng 104 độ góc b bằng với
- góc e cùng bằng 47 độ và cuối cùng góc C
- bằng với góc f bằng 29 đ
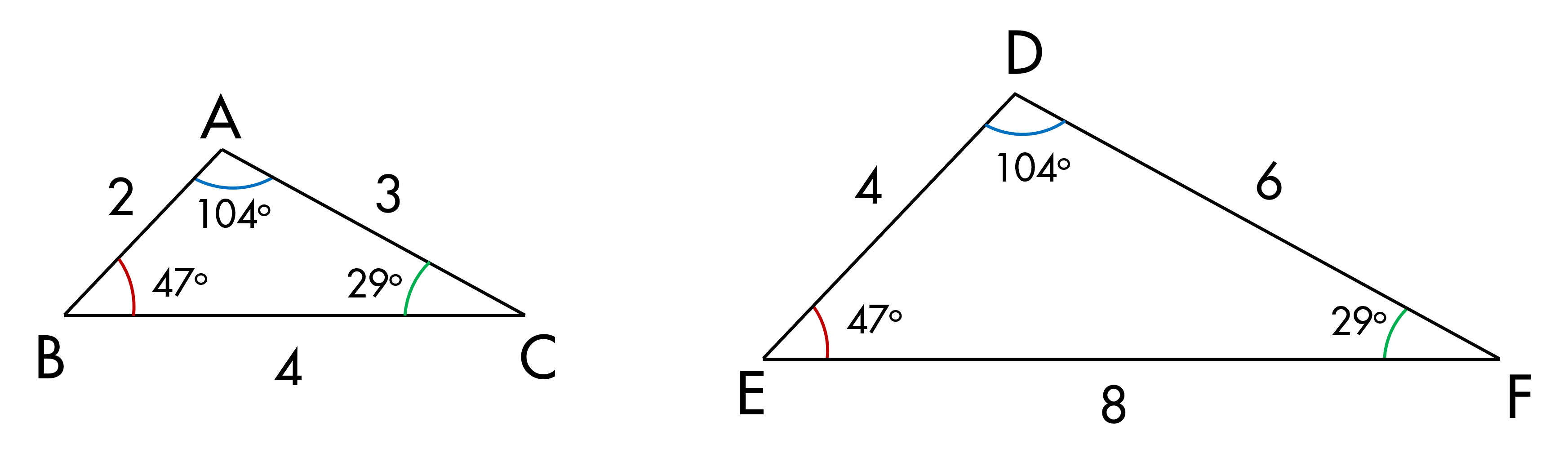
- câu hỏi số 2 tính và so sánh các tỉ số
- sau tỷ số AB trde AC tr df và BC tr
- EF AB tr de bằng
- 2/4 ac tr df Bằng 3/6 và BC trên EF bằng
- 4/8
- như vậy sau khi rút gọn chúng ta có thể
- thấy ba tỉ số này bằng nhau và bằng
- 1/2 sau khi hoàn thành nhiệm vụ A và B
- chúng ta có thể thấy hai tam giác này có
- các góc tương ứng bằng nhau và các cạnh
- tương ứng tỉ lệ và cụ thể hơn là tỉ lệ
- 1/2 như vậy tam giác abc được gọi là
- đồng dạng với tam giác DEF Nếu chúng ta
- chỉ ra được hai điều sau đây đó là các
- góc tương ứng bằng nhau góc A và góc D
- góc góc B bằng góc e góc C bằng góc f và
- các cạnh tương ứng tỉ lệ là ab trde bằng
- ac tr df bằ BC tr EF và nói chung khi
- chúng ta chứng minh hai tam giác đồng
- dạng Hiện tại thì ta cần phải chỉ ra các
- cặp góc tương ứng bằng nhau và các cạnh
- tương ứng tỉ lệ về mặt ký hiệu thì giống
- như tam giác bằng nhau chúng ta sẽ ký
- hiệu theo các đỉnh tương
- ứng ta sẽ ký hiệu là tam giác ABC đồng
- dạng với tam giác DEF đây là ký hiệu
- đồng dạng
- ạ Và nếu như các cạnh tương ứng có tỉ số
- bằng
- k thì ta gọi tỷ số k là tỷ số đồng dạng
- của tam giác ABC và tam giác DEF một lưu
- ý khi chúng ta tính tỷ số k của hai tam
- giác đồng dạng tam giác nào viết trước
- thì chúng ta sẽ lấy cạnh của tam giác đó
- là tử số tam giác nào viết sau ta sẽ lấy
- cạnh của tam giác đó là mẫu
- số tiếp theo chúng ta sẽ sang phần luyện
- tập bài tập số 2 phần A tam giác nào
- đồng dạng với tam giác
- ABC ở trên hình vẽ thì chúng ta có thể
- thấy tam giác ABC không có góc vuông nào
- mà tam giác ghj lại có một góc vuông do
- đó tam giác này không thể đồng dạng với
- tam giác ABC
- như vậy chúng ta chỉ xét hai tam giác
- ABC và tam giác
- MNP để chỉ ra hai tam giác ABC và MNP
- đồng dạng thì ta cần chỉ ra các góc
- tương ứng bằng nhau và các cạnh tương
- ứng tỉ lệ về các góc tương ứng bằng nhau
- thì chúng ta thấy góc A bằng với góc
- M Góc B bằng với Góc N và áp dụng định
- lý tổng ba góc của một tam giác bằng 180
- độ chúng ta hoàn toàn có thể chứng minh
- được góc C bằng góc p về phần này các em
- có thể tự chứng
- minh tiếp theo là chúng ta cần phải chỉ
- ra các cạnh tướng tỉ lệ cụ thể hơn cạnh
- nhỏ nhất của tam giác ABC sẽ tương ứng
- với cạnh nhỏ nhất của tam giác MNP tương
- tự với cạnh nhỏ thứ hai và cạnh nhỏ thứ
- ba của hai tam giác
- này và tỷ số đầu tiên sẽ là cạnh nhỏ
- nhất là ab chia cho
- MN bằng
- 4/6 cạnh nhỏ thứ hai là BC chia cho NP
- là 5 chia 7,5 và cuối cùng là cạnh lớn
- nhất là
- AC trên MP là 7/1
- ph5 và sau khi tính các tỉ số này chúng
- ta thấy các tỷ số này đều bằng
- 2/3 như vậy hai tam giác này có các cạnh
- tương ứng tỉ lệ từ đây ta kết luận tam
- giác ABC đồng dạng với tam giác
- daf sang đến câu b
- Chúng ta sẽ cùng nhau Tính tỉ số đồng
- dạng của tam giác MNP và tam giác
- ABC vì tam giác MNP là tam giác viết
- trước thế nên tỷ số đồng dạng của tam
- giác MNP với tam giác ABC sẽ bằng cạnh
- của tam giác MNP ta có thể chọn cạnh bất
- kỳ là cạnh
- MN cạnh tương ứng với nó sẽ là cạnh AB
- MN tr AB sẽ bằng
- 6/4 và bằng 3/2 như vậy tỷ số k bằng 3/2
- đến đây Chúng ta có một số nhận xét như
- sau nếu tam giác ABC đồng dạng với tam
- giác
- a'b'c' với tỉ số đồng dạng là k thì tam
- giác a'b'c' sẽ đồng dạng với tam giác
- ABC với tỉ số 1
- trk đây là khi chúng ta viết ngược lại
- các vị trí của hai tam giác đồng dạng
- thì tỷ số sẽ bị nghịch đả nhận xét thứ
- hai là hai tam giác bằng nhau thì đồng
- dạng với nhau theo tỉ số đồng dạng K = 1
- và đặc biệt mọi tam giác sẽ đồng dạng
- với chính
- nó hai tam giác bằng nhau thì các cạnh
- tương ứng bằng nhau Do đó tỉ số đồng
- dạng K sẽ bằng
- 1 và cuối cùng nếu tam giác ABC đồng
- dạng với tam giác
- a'b'c' với tỉ số đồng dạng là k và tam
- giác a'b'c' đồng dạng với tam giác a2 b2
- c2 với tỉ số đồng dạng là h thì tam giác
- ABC đồng dạng với tam giác a2 b2 c2 với
- tỉ số đồng dạng là m = k x h
- đây là tính chất bắc cầu của các tam
- giác đồng dạng tam giác thứ nhất đồng
- dạng với tam giác thứ hai và tam giác
- thứ hai đồng dạng với tam giác thứ ba
- thì tam giác thứ nhất sẽ đồng dạng với
- tam giác thứ ba với tỉ số đồng dạng sẽ
- bằng tích hai tỉ số đồng dạng tương
- ứng chúng ta có thể làm rõ hơn về nhận
- xét này bằng cách chúng ta sẽ viết từng
- tỷ số đồng dạng K và m dưới dạng tỉ số
- của các
- cạnh cụ thể Dể hơn với cặp đầu tiên
- chúng ta sẽ có tỉ số đồng dạng là k = AB
- tr
- a'b' cặp tam giác thứ hai sẽ là h bằ
- a'b' chia A2 tr B2 và cuối cùng là m
- bằng AB chia cho A2 và
- B2 như vậy khi chúng ta lấy K nh h ta sẽ
- lấy ab trên a'b' nhân với a'b' trên a2
- b2 và rút gọn ta sẽ được AB tr A2 ph B2
- và chính bằng
- m Vậy là chúng ta đã chứng minh xong
- nhận xét thứ
- ba và đây cũng là nội dung cuối cùng
- thầy mang đến cho các em ở trong phần
- này Và bây giờ chúng ta sẽ cùng nhau đến
- với câu hỏi tương tác để củng cố các
- phần chúng ta vừa
- học I
Bạn có thể đăng câu hỏi về bài học này ở đây

