Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 2 (phần tự luận 7 điểm) SVIP
Bài 1. (2 điểm) Cho biểu thức $A=\dfrac{{{x}^{2}}}{{{x}^{2}}-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}.$
a) Viết điều kiện xác định của biểu thức $ A.$
b) Rút gọn biểu thức $A$.
c) Tìm giá trị của $x$ để $A=2.$
Hướng dẫn giải:
a) Điều kiện xác định của biểu thức $A$ là: ${{x}^{2}}-4\ne 0;\,\,x-2\ne 0$ và $x+2\ne 0$
Mà ${{x}^{2}}-4=\left( x-2 \right)\left( x+2 \right)$
Vậy điều kiện xác định của biểu thức $A$ là $x-2\ne 0$ và $x+2\ne 0$ hay $x\ne 2$ và $x \ne -2$.
b) Với điều kiện xác định $x\ne 2$ và $x \ne -2$ ta có:
$A=\dfrac{2{{x}^{2}}}{{{x}^{2}}-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}$
$=\dfrac{2{{x}^{2}}}{\left( x-2 \right)\left( x+2 \right)}-\dfrac{x\left( x+2 \right)}{\left( x-2 \right)\left( x+2 \right)}-\dfrac{2\left( x-2 \right)}{\left( x+2 \right)\left( x-2 \right)}$
$=\dfrac{2{{x}^{2}}-{{x}^{2}}-2x-2x+4}{\left( x-2 \right)\left( x+2 \right)}$
$=\dfrac{{{x}^{2}}-4x+4}{\left( x-2 \right)\left( x+2 \right)}$
$=\dfrac{{{\left( x-2 \right)}^{2}}}{\left( x-2 \right)\left( x+2 \right)}$
$=\dfrac{x-2}{x+2}.$
c) Với $x\ne 2,$ và $x \ne -2$ để $A=2$ thì $\dfrac{x-2}{x+2}=2$
Suy ra $x-2=2\left( x+2 \right)$
Do đó $x-2=2x+4$ hay $x=-6$ (thỏa mãn điều kiện)
Vậy $x=-6.$
Bài 2. (1 điểm) Phân tích các đa thức sau thành nhân tử:
a) ${{x}^{2}}-2x+1-{{y}^{2}}$;
b) ${{x}^{2}}-8x+12$.
Hướng dẫn giải:
a) ${{x}^{2}}-2x+1-{{y}^{2}}$
$=\left( {{x}^{2}}-2x+1 \right)-{{y}^{2}}$
$={{\left( x-1 \right)}^{2}}-{{y}^{2}}$
$=\left( x-1-y \right)\left( x-1+y \right).$
b) ${{x}^{2}}-8x+12$
$={{x}^{2}}-2x-6x+12$
$=\left( {{x}^{2}}-2x \right)-\left( 6x-12 \right)$
$=x\left( x-2 \right)-6\left( x-2 \right)$
$=\left( x-2 \right)\left( x-6 \right).$
Bài 3. (1,0 điểm) Từ một khúc gỗ hình lập phương cạnh $30$ cm. Người ta cắt đi một phần gỗ để được phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh $30$ cm và chiều cao của hình chóp cũng bằng $30$ cm. Tính thể tích của phần gỗ bị cắt đi.
Hướng dẫn giải:
Thể tích khúc gỗ hình lập phương là: ${{30}^{3}}=27 \, 000$ (cm3).
Thể tích của phần gỗ còn lại hình chóp tứ giác đều là: $\dfrac{1}{3}{{.30}^{2}}.30=9 \, 000$ (cm3).
Thể tích của khối gỗ bị cắt đi là: $27 \, 000-9 \, 000=18 \, 000$ (cm3).
Bài 4. (2 điểm)
a) Tìm số đo $x$ trong hình vẽ sau.

b) Một chiếc thang có chiều dài $AB=3,7$ m đặt cách một bức tường khoảng cách $BH=1,2$ m.
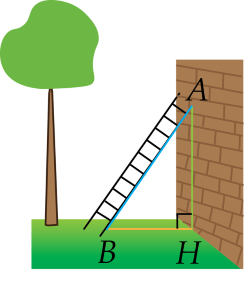
Hỏi khoảng cách đặt thang cách chân tường là $BH$ có "an toàn" không? Biết rằng khoảng cách "an toàn" khi $2,0<\dfrac{AH}{BH}<2,2$.
Hướng dẫn giải:
a) Góc ngoài tại đỉnh $B$ có số đo bằng $70^\circ $ nên góc trong tại đỉnh $B$ có số đo bằng $180^\circ -70^\circ =110^\circ $
Xét tứ giác $ABCD,$ ta có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^\circ $
Do đó $3x+110^\circ +x+90^\circ =360^\circ $
uy ra $4x=160^\circ $ nên $x=40^\circ $
Vậy $x=40^\circ $.
b) Áp dụng định lí Pythagore vào tam giác ${ABH}$ vuông tại ${H}$ ta có: $A B^2=A H^2+B H^2$
Suy ra $A{{H}^{2}}=A{{B}^{2}}-B{{H}^{2}}$
Do đó $AH=\sqrt{A{{B}^{2}}-B{{H}^{2}}}=\sqrt{3,{{7}^{2}}-1,{{2}^{2}}}=3,5$ m
Ta có $\dfrac{A H}{B H}=\dfrac{3,5}{1,2} \approx 2,9$
Mà $2,9>2,2$ nên khoảng cách đặt thang cách chân tường đã cho là không an toàn.
Bài 5. (1 điểm) Tìm giá trị lớn nhất của biểu thức $A = 5 + 2xy + 14y - x^2 - 5y^2 - 2x$.
Hướng dẫn giải:
$ A=5+2xy+14y-{{x}^{2}}-5{{y}^{2}}-2x$
$=-\left( {{x}^{2}}+{{y}^{2}}+1-2xy-2y+2x \right)-\left( 4{{y}^{2}}-12y+9 \right)+15 $
$=-{{\left( x-y+1 \right)}^{2}}-{{\left( 2y-3 \right)}^{2}}+15\le 15$
Suy ra giá trị lớn nhất của $A=15$ khi và chỉ khi:
$ x-y=-1$ và $2y-3=0$
Suy ra $x=\dfrac{1}{2}$ và $y=\dfrac{3}{2} $.
