Dạng vô định 0/0 SVIP

Xét bài toán: Tính $\lim\limits _{x \rightarrow x_0} \dfrac{f(x)}{g(x)}$ khi $\lim\limits _{x \rightarrow x_0} f(x)=\lim\limits _{x \rightarrow x_0} g(x)=0$, trong đó $f(x), g(x)$ là các đa thức và căn thức.

Phương pháp giải:

Phân tích tử và mẫu thành các nhân tử và giản ước: $\lim\limits _{x \rightarrow x_0} \dfrac{f(x)}{g(x)}=\lim\limits _{x \rightarrow x_0} \dfrac{\left(x-x_0\right) \cdot A(x)}{\left(x-x_0\right) \cdot B(x)}=\lim\limits _{x \rightarrow+\infty} \dfrac{A(x)}{B(x)}$.

Nếu $A(x), B(x)$ đều chứa nhân tử $x-x_0$ ta sẽ tiếp tục phân tích thành các nhân tử.

Dạng 1: Phân tích các đa thức ở tử và mẫu thành nhân tử rồi rút gọn

Ví dụ 1: Tính $\lim\limits _{x \rightarrow 1} \dfrac{x^2-3 x+2}{x-1}$.

Giải

Cách 1:

$\lim\limits  _{x \rightarrow 1} \dfrac{x^2-3 x+2}{x-1}=\lim\limits _{x \rightarrow 1} \dfrac{(x-1)(x-2)}{x-1}=\lim\limits _{x \rightarrow 1}(x-2)=-1 .$

Cách 2: (Trắc nghiệm)

Nhập vào màn hình $\dfrac{X^2-3 X+2}{X-1}$ ấn CALC $1+10^{-10} =$ ta được kết quả

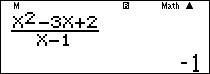
Dạng 2: Nhân thêm lượng liên hợp với biểu thức chứa căn

Ví dụ 2: Tính $\lim\limits _{x \rightarrow 0} \dfrac{\sqrt{1+x}-1}{x}$.

Giải

Cách 1: Nhân thêm lượng liên hợp với biểu thức tử

$\lim\limits _{x \rightarrow 0} \dfrac{\sqrt{1+x}-1}{x}=\lim\limits _{x \rightarrow 0} \dfrac{1+x-1}{x(\sqrt{1+x}+1)}=\lim\limits _{x \rightarrow 0} \dfrac{1}{\sqrt{1+x}+1}=\dfrac{1}{2} \text {. }$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\dfrac{\sqrt{1+x}-1}{x}$ ấn CALC $0+10^{-5} =$ ta được kết quả $\approx \dfrac{1}{2}$.

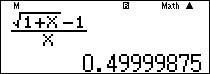
Dạng 3: Thêm bớt hằng số hoặc biểu thức chứa biến đơn giản rồi nhân liên hợp

Ví dụ 3: Tính giới hạn  $\lim\limits_{x \rightarrow 0} \dfrac{2 \sqrt{1+x}-\sqrt[3]{8-x}}{x}$.

Giải:

Nhận xét: Việc nhân thêm lượng liên hợp của tử số tương đối phức tạp do các căn thức có bậc khác nhau. Ta nhẩm tính, với $x=0$ thì $2 \sqrt{1+x} = 2$ và $\sqrt[3]{8-x} = 2$, vậy ta sẽ thêm bớt $2$ rồi khử căn như sau:

Ta có: 

$\begin{aligned} &\lim\limits _{x \rightarrow 0} \dfrac{2 \sqrt{1+x}-\sqrt[3]{8-x}}{x}=\lim\limits _{x \rightarrow 0}\left(\dfrac{2 \sqrt{1+x}-2}{x}+\dfrac{2-\sqrt[3]{8-x}}{x}\right) \\ & =\lim\limits _{x \rightarrow 0}\left(\dfrac{2}{\sqrt{x+1}+1}+\dfrac{1}{4+2 \sqrt[3]{8-x}+\sqrt[3]{(8-x)^2}}\right)=1+\dfrac{1}{12}=\dfrac{13}{12} .\end{aligned}$