Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài toán ứng dụng thực tiễn của giới hạn dãy số SVIP
Cho tam giác đều ABC có độ dài cạnh bằng 1. Nối các trung điểm A1,B1,C1 của các cạnh BC,CA,AB ta được tam giác đều A1B1C1. Tiếp tục nối các trung điểm A2,B2,C2 của các cạnh B1C1,C1A1,A1B1 ta được tam giác đều A2B2C2, thực hiện quá trình này đến vô hạn.
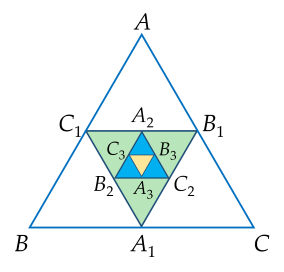
Gọi Sn lần là diện tích của tam giác đều AnBnCn.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tam giác A1B1C1 có độ dài các cạnh bằng 21. |
|
| b) Biết rằng tam giác đều có cạnh bằng a thì có diện tích là 4a23. Diện tích tam giác A3B3C3 là S3=643. |
|
| c) Đặt un=S1+S2+S3+...+Sn. Khi đó limun=123. |
|
| d) Đặt h1=AA1,h2=A1A2,h3=A2A3,...,hn=An−1An và vn=h1+h2+...+hn. Khi đó limvn=3. |
|
Một bệnh nhân hàng ngày phải uống một viên thuốc 100 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn tồn dư 5%.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Ngay trước khi uống viên thuốc ngày thứ hai, hàm lượng thuốc trong cơ thể là 100 mg. |
|
| b) Ngay sau khi uống viên thuốc ngày thứ hai, hàm lượng thuốc trong cơ thể là 105 mg. |
|
| c) Hàm lượng thuốc trong cơ thể sau khi uống viên thuốc ngày thứ tư là 105,2625 mg. |
|
| d) Nếu sử dụng thuốc lâu ngày thì hàm lượng thuốc trong cơ thể hằng ngày được ước tính theo công thức 100(1+5%) mg. |
|
Xét quá trình tạo ra hình vuông như sau: Bắt đầu hằng một hình vuông H0 cạnh bằng 1 đơn vị độ dài. Chia hình vuông H0 thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình h1. Tiếp theo, chia mỗi hình vuông của h1 thành chín hình vuông rồi bỏ đi bốn hình vuông, nhận được hình h2. Tiếp tục quá trình này, ta nhận được một dãy hình hn(n=1,2,3,...).

Xét un là cạnh của mỗi hình vuông tương ứng với hình hn,(n=1,2,3,...).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) u1=31. |
|
| b) u2=21. |
|
| c) un lập thành cấp số nhân lùi vô hạn với công bội q=31. |
|
| d) Gọi Sn là tổng diện tích tất cả các hình vuông ở hình hn. Khi đó limSn=0. |
|
Cho hình vuông ABCD có cạnh bằng a1 và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2, B2, C2, D2 có diện tích S3, …và cứ tiếp tục làm như thế.

Giả sử quá trình trên kéo dài vô hạn. Tính tổng diện tích (đơn vị cm2) các hình vuông được tạo thành biết a1=4 cm.
Trả lời:
Cho tam giác OMN vuông cân tại O, OM=ON=5. Trong tam giác OMN, vẽ hình vuông OA1B1C1 sao cho các đỉnh A1;B1;C1 lần lượt nằm trên các cạnh OM;MN;ON. Trong tam giác A1MB1, vẽ hình vuông A1A2B2C2 sao cho các đỉnh A1;B2;C2 lần lượt nằm trên các cạnh A1M;MB1;A1B1.
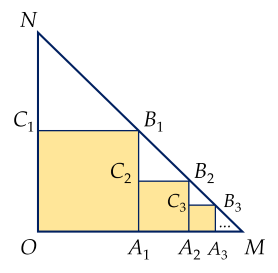
Tiếp tục quá trình đó mãi mãi, ta được một dãy các hình vuông (tham khảo hình vẽ). Tính tổng diện tích các hình vuông này. (Làm tròn kết quả đến chữ số hàng phần mười)
Trả lời:
Trong một nhà máy, người ta đo được rằng 90% lượng nước sau khi sử dụng được xử lí và tái sử dụng. Khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, để nhà máy sử dụng được tổng lượng nước là 1 000 (m3) thì cần có bao nhiêu mét khối nước ban đầu được sử dụng?
Trả lời:
Từ độ cao 63 m của một ngọn tháp, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 101 độ cao mà quả bóng đạt được ngay trước đó. Độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất (khi khoảng cách từ quả bóng đến mặt đất không đáng kể) là bao nhiêu mét?
Trả lời:
Từ tờ giấy, cắt một hình tròn bán kính R=2 (cm) như hình vẽ. Tiếp theo, cắt hai hình tròn bán kính 2R chồng lên hình tròn đầu tiên.
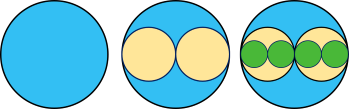
Tiếp theo, cắt bốn hình tròn bán kính 4R rồi chồng lên các hình trước. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn. (làm tròn kết quả đến hàng phần mười)
Trả lời:
Ông Đô dự định dùng xen kẽ hai màu vàng, xanh để sơn trang trí một bức tường hình chữ nhật theo cách như sau: Đầu tiên dùng màu vàng sơn bức tường theo tấm bìa hình chữ nhật H1 có chiều dài, chiều rộng tính theo đơn vị m lần lượt là 5+1 và 2, sau đó cắt hình H1 thành một hình vuông có cạnh bằng chiều rông của H1 và hình chữ nhật H2, rồi dùng màu xanh sơn tường theo hình H2, …cứ tiếp tục quá trình như vậy cho đến khi hình chữ nhật tạo ra có diện tích không đáng kể.
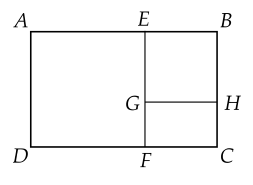
Biết rằng tiền công để sơn mỗi mét vuông tường như vậy là 21 nghìn đồng. Ông Đô cần chuẩn bị tối đa bao nhiêu tiền công cho thợ sơn? (kết quả tính theo đơn vị nghìn đồng và làm tròn đến hàng nghìn).
Trả lời:
Cho hình vuông C1 có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (hình vẽ).

Từ hình vuông C2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông C1,C2,C3,...,Cn. Gọi Si là diện tích của hình vuông Ci, (i∈{1;2;3;...;n}). Khi đó lima22025(S1+S2+...+Sn) bằng bao nhiêu?
Trả lời:
Một mô hình gồm các khối cầu xếp chồng lên nhau tạo thành một cột thẳng đứng. Biết rằng mỗi khối cầu có bán kính gấp đôi khối cầu nằm ngay trên nó và bán kính khối cầu dưới cùng là 50 cm. Chiều cao mô hình dưới x mét, x là số tự nhiên, đơn vị cm. Tìm x.
Trả lời:
Trong một lần Đoàn trường THPT Giao Thủy C tổ chức chơi bóng chuyền hơi, bạn Nam thả một quả bóng chuyền hơi từ tầng ba, độ cao 8 m so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với mặt đất. Khi đó tổng quãng đường (đơn vị mét) quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy nữa gần bằng số tự nhiên nào?
Trả lời:


Bạn có thể đánh giá bài học này ở đây