cho hai đa thức P(x)=-6x5 -4x4 +3x2 -2x ;Q(x)=2x5 -4x4 -2x3 -2x2 -x -3 Gọi M(x)=P(x)-Q(x). Tính M(-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{B}+\widehat{C}=180^0-75^0=105^0\)
mà \(\widehat{B}-\widehat{C}=15^0\)
nên \(\widehat{B}=\dfrac{105^0+15^0}{2}=60^0;\widehat{C}=60^0-15^0=45^0\)
b: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{60^0}{2}=30^0\)
Xét ΔABD có \(\widehat{ABD}+\widehat{BAD}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}+30^0+75^0=180^0\)
=>\(\widehat{ADB}=75^0\)


c: Đặt \(\left(x-4\right)\left(x-1\right)\left(x+2\right)^2=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x-1=0\\\left(x+2\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=4\\x=1\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\\x=-2\end{matrix}\right.\)
k: Đặt \(x^2-4x+3=0\)
=>\(x^2-x-3x+3=0\)
=>x(x-1)-3(x-1)=0
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: MK//AC
=>\(\widehat{KMA}=\widehat{MAC}\)
mà \(\widehat{MAC}=\widehat{KAM}\)
nên \(\widehat{KMA}=\widehat{KAM}\)
=>ΔKAM cân tại K
=>KA=KM
Ta có: KM//AC
=>\(\widehat{KMB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)
nên \(\widehat{KMB}=\widehat{KBM}\)
=>KM=KB
mà KM=KA
nên KB=KA
=>K là trung điểm của AB
c: ΔAMB=ΔAMC
=>MB=MC
=>M là trung điểm của BC
Xét ΔABC có
AM,CK là các đường trung tuyến
AM cắt CK tại H
Do đó: H là trọng tâm của ΔABC
=>BH cắt AC tại trung điểm của AC
=>E là trung điểm của AC
Trên tia đối của tia EB, lấy N sao cho EN=EB
Xét ΔEBC và ΔENA có
EB=EN
\(\widehat{BEC}=\widehat{NEA}\)
EC=EA
Do đó: ΔEBC=ΔENA
=>BC=AN
Xét ΔABN có AB+AN>BN
mà AN=BC và BN=2BE
nên BA+BC>2BE

Để so sánh hai số 0.25 và 0.6, ta có thể sử dụng các cách sau:
1. So sánh trực tiếp:
Nhìn vào hai số, ta có thể thấy 0.6 lớn hơn 0.25.
2. Vẽ số trên trục số:
-
Vẽ trục số và đánh dấu các điểm 0, 0.25 và 0.6.
-
Qua hình vẽ, ta thấy điểm 0.6 nằm xa điểm 0 hơn so với điểm 0.25. Do đó, 0.6 lớn hơn 0.25.
3. Sử dụng biểu đồ số:
- Vẽ biểu đồ số với hai thanh có chiều cao tương ứng với 0.25 và 0.6. So sánh 0.25 và 0.6 bằng biểu đồ số
- Chiều cao của thanh 0.6 cao hơn so với thanh 0.25. Do đó, 0.6 lớn hơn 0.25.
Kết luận:
Bằng cả ba cách so sánh trên, ta có thể cho thấy: 0.6 lớn hơn 0.25.
Ngoài ra, ta cũng có thể sử dụng các phép toán sau để so sánh hai số:
- 0.6 - 0.25 = 0.35 > 0
- 0.25 / 0.6 = 0.4167 < 1
Cả hai phép toán này đều cho ta kết quả 0.6 lớn hơn 0.25.

Thể tích của chiếc thùng là:
\(30\cdot20\cdot15=9000\left(cm^3\right)\)
Thể tích của mỗi hộp bánh là:
\(10\cdot10\cdot10=1000\left(cm^3\right)\)
Chiếc thùng có thể đựng được số chiếc bánh là:
\(9000:1000=9\) (chiếc)
Bạn phải xem xem có thể xếp được 9 hộp bánh đó vào thùng được không. Thùng có chiều cao 15cm nhưng mỗi hộp bánh lại có chiều cao 10cm nên không thể xếp các hộp bánh thành 2 tầng được mà chỉ xếp được 1 tầng hộp bánh mà thôi. Trong trường hợp đó, số hộp bánh tối đa mà hộp chứa được là \(\dfrac{20.30}{10.10}=6\) hộp nhé.

x, y là 2 đại lượng tỉ lệ nghịch nên ta có: \(xy=k=>k=4\cdot1,5=6\)
\(x=0,5=>y=\dfrac{k}{x}=\dfrac{6}{0,5}=12\)
\(x=-1,2=>y=\dfrac{k}{x}=\dfrac{6}{-1,2}=-5\)
\(y=3=>x=\dfrac{k}{y}=\dfrac{6}{3}=2\)
\(y=-2=>x=\dfrac{k}{y}=\dfrac{6}{-2}=-3\)
| x | 0,5 | -1,2 | 2 | -3 | 4 |
| y | 12 | -5 | 3 | -2 | 1,5 |

x và y là 2 đại lượng tỉ lệ nghịch nên: \(xy=k=>k=-2\cdot-15=30\)
\(x=10=>y=\dfrac{k}{x}=\dfrac{30}{10}=3\)
\(y=-3=>x=\dfrac{30}{-3}=-10\)
\(x=15=>y=\dfrac{k}{x}=\dfrac{30}{15}=2\)
\(y=5=>x=\dfrac{k}{y}=\dfrac{30}{5}=6\)
| x | -2 | 10 | -10 | 15 | 6 |
| y | -15 | 3 | -3 | 2 | 5 |

\(\left[\left(-\dfrac{1}{2}\right)^3-\left(\dfrac{3}{4}\right)^3\cdot\left(-2\right)^2\right]:\left[2\cdot\left(-1\right)^5+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\right]\\ =\left(-\dfrac{1}{8}-\dfrac{27}{64}\cdot4\right):\left(2\cdot-1+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(-\dfrac{1}{8}-\dfrac{27}{16}\right):\left(-2+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(\dfrac{-2}{16}-\dfrac{27}{16}\right):\left(\dfrac{-32}{16}+\dfrac{9}{16}-\dfrac{6}{16}\right)\\ =\dfrac{-29}{16}:\dfrac{-29}{16}\\ =1\)
____________________________
\(\left[3\dfrac{1}{6}-\left(0,06\cdot7\dfrac{1}{2}+6\dfrac{1}{4}\cdot0,24\right)\right]:\left(1\dfrac{2}{3}+2\dfrac{2}{3}\cdot1\dfrac{3}{4}\right)\\ =\left[\dfrac{19}{6}-\left(0,06\cdot\dfrac{15}{2}+\dfrac{25}{4}\cdot4\cdot0,06\right)\right]:\left(\dfrac{5}{3}+\dfrac{8}{3}\cdot\dfrac{7}{4}\right)\\ =\left[\dfrac{19}{6}-0,06\cdot\left(\dfrac{15}{4}+25\right)\right]:\left(\dfrac{5}{3}+\dfrac{14}{3}\right)\\ =\left(\dfrac{19}{6}-0,06\cdot\dfrac{65}{2}\right):\dfrac{19}{3}\\ =\left(\dfrac{19}{6}-\dfrac{39}{20}\right):\dfrac{19}{3}\\ =\dfrac{73}{60}:\dfrac{19}{3}\\ =\dfrac{73}{380}\)




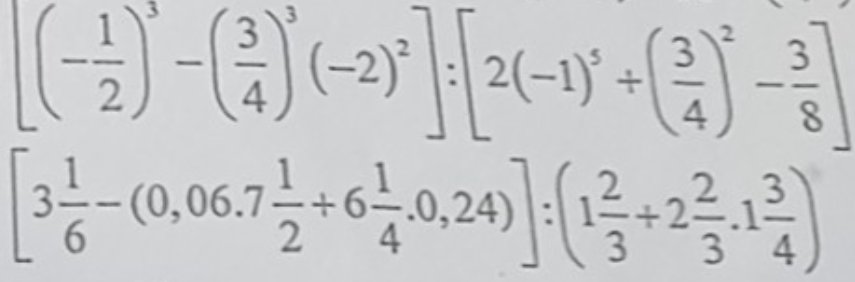
M(x)=P(x)-Q(x)
\(=-6x^5-4x^4+3x^2-2x-2x^5+4x^4+2x^3+2x^2+x+3\)
\(=-8x^5+2x^3+5x^2-x+3\)
\(M\left(-1\right)=-8\left(-1\right)^5+2\cdot\left(-1\right)^3+5\cdot\left(-1\right)^2-\left(-1\right)+3\)
=8-2+5+1+3
=6+6+3
=15