 Giúp e với ạ e cần gấp lắm, e cảm ơn trước
Giúp e với ạ e cần gấp lắm, e cảm ơn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(\left(-56\right)+74+\left(-14\right)+56\)
=(-56+56)+(74-14)
=0+60
=60
2: \(\left(-12\right)+89+\left(-28\right)=89-\left(12+28\right)\)
=89-40
=49
3: \(\left(-5\right)+\left(-75\right)+100+\left(-20\right)\)
=-80-20+100
=-100+100=0
4: \(\left(-27\right)+\left(-208\right)+\left(-43\right)+\left(-102\right)\)
\(=\left(-27-43\right)+\left(-208-102\right)\)
=-70-310
=-380
5: \(\left(-105\right)\cdot19+\left(-76\right)\cdot105-5\cdot105\)
\(=\left(-105\right)\left(19+76+5\right)\)
\(=-105\cdot100=-10500\)
6: \(140+4\cdot119-4\cdot19\)
\(=140+4\cdot\left(119-19\right)\)
\(=140+4\cdot100=140+400=540\)
7: \(\left(2022-129+537\right)-\left(-129+637\right)\)
=2022-129+537+129-637
=2022-100
=1922
8: \(\left(2022-3015\right)-\left(85-2022\right)-\left(-500\right)\)
=2022-3015-85+2022+500
=4044-3100+500
=4044-2600
=1444
9: \(2814:14-\left(23\cdot52-156\right)\cdot2\)
\(=201-52\left(23-3\right)\cdot2\)
\(=201-52\cdot20\cdot2=201-52\cdot40=-1879\)
10: \(\left[516-\left(25\cdot4+16\right)\right]:8-68\)
\(=\left[516-100-16\right]:8-68\)
\(=400:8-68=50-68=-18\)
11: \(5\cdot32+60:2^2-\left(11-6\right)^2\)
\(=160+60:4-5^2\)
=160+15-25
=160-10
=150
12: \(160-10\cdot\left[128-\left(12-3\right)^2\right]-2021^0\)
\(=160-10\cdot\left(128-9^2\right)-1\)
\(=159-10\cdot\left(128-81\right)=159-10\cdot47\)
=159-470
=-311
13: \(5\cdot6^2+240:4^2-3\left(17-12\right)^2\)
\(=5\cdot36+240:16-3\cdot5^2\)
=180+15-75
=180-60
=120
14: 1-2+3-4+...+99-100
=(1-2)+(3-4)+...+(99-100)
=(-1)+(-1)+...+(-1)
=-50

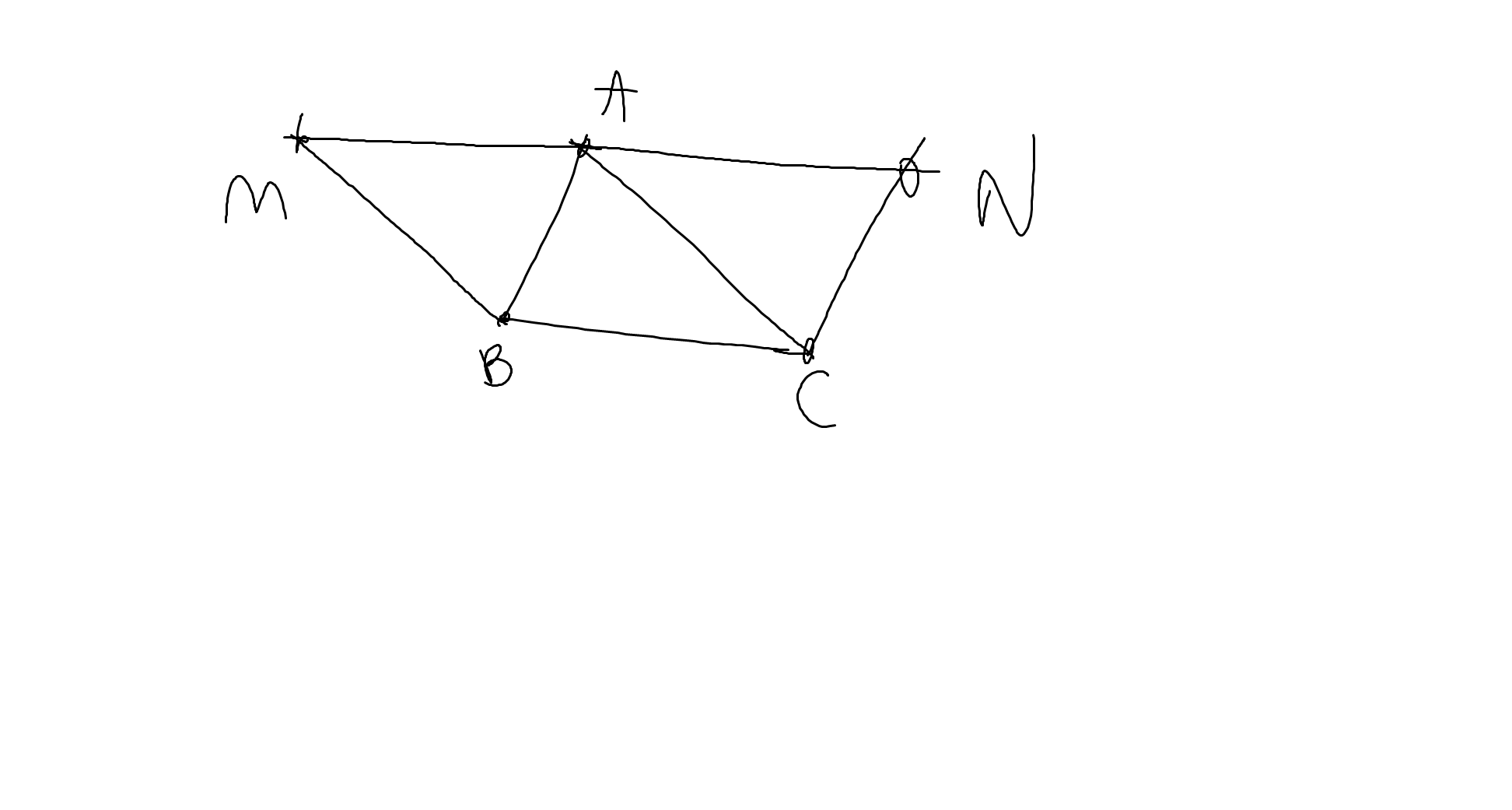
a: Xét ΔMAB và ΔCBA có
\(\widehat{MAB}=\widehat{ABC}\)(hai góc so le trong, MA//BC)
AB chung
\(\widehat{ABM}=\widehat{BAC}\)(hai góc so le trong, MB//AC)
Do đó;ΔMAB=ΔCBA
Xét ΔABC và ΔCNA có
\(\widehat{BAC}=\widehat{NCA}\)(hai góc so le trong, BA//CN)
AC chung
\(\widehat{BCA}=\widehat{NAC}\)(hai góc so le trong, AN//BC)
Do đó: ΔABC=ΔCNA
b: ΔMAB=ΔCBA
=>MA=CB
ΔABC=ΔCNA
=>BC=NA
mà BC=AM
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN

Bài 3:
a: \(2^x+2^{x+1}+...+2^{x+100}=2^{101}-1\)
=>\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)
Đặt \(A=1+2+...+2^{100}\)
=>\(2A=2+2^2+...+2^{101}\)
=>\(2A-A=2+2^2+...+2^{101}-1-2-...-2^{100}\)
=>\(A=2^{101}-1\)
\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)
=>\(2^x\left(2^{101}-1\right)=2^{101}-1\)
=>\(2^x=1=2^0\)
=>x=0
b: p là số nguyên tố lớn hơn 3 nên \(\left\{{}\begin{matrix}p⋮̸2\\p⋮̸3\end{matrix}\right.\)
p không chia hết cho 3 nên p=3k+1 hoặc p=3k+2
TH3: p=3k+1
\(\left(p-1\right)\left(p+1\right)\)
\(=\left(3k+1-1\right)\left(3k+1+1\right)\)
\(=3k\left(3k+2\right)⋮3\)(3)
TH2: p=3k+2
\(\left(p-1\right)\left(p+1\right)=\left(3k+2-1\right)\left(3k+2+1\right)\)
\(=\left(3k+1\right)\left(3k+3\right)=3\left(k+1\right)\left(3k+1\right)⋮3\)(2)
Từ (2),(3) suy ra \(\left(p-1\right)\left(p+1\right)⋮3\)
p không chia hết cho 2 nên p=2k+1
\(\left(p-1\right)\left(p+1\right)=\left(2k+1-1\right)\left(2k+1+1\right)\)
\(=2k\left(2k+2\right)=4k\left(k+1\right)\)
Vì k;k+1 là hai số nguyên liên tiếp
nên \(k\left(k+1\right)⋮2\)
=>\(4k\left(k+1\right)⋮4\cdot2\)
=>\(4k\left(k+1\right)⋮8\)
=>\(\left(p-1\right)\left(p+1\right)⋮8\)
mà \(\left(p-1\right)\left(p+1\right)⋮3\)
và ƯCLN(3;8)=1
nên \(\left(p-1\right)\left(p+1\right)⋮3\cdot8=24\)

Diện tích bức tường là \(15\cdot4=60\left(m^2\right)\)
Diện tích hai cửa sổ hình chữ nhật là:
\(1,8\cdot1,5\cdot2=1,8\cdot3=5,4\left(m^2\right)\)
Diện tích cửa chớp hình vuông là \(0,5^2=0,25\left(m^2\right)\)
Diện tích cần sơn là:
\(60-5,4-0,25=54,35\left(m^2\right)\)
Số tiền cần phải trả là:
\(54,35\cdot50000=2717500\left(đồng\right)\)

Diện tích bức tường là \(15\cdot4=60\left(m^2\right)\)
Diện tích hai cửa sổ hình chữ nhật là:
\(1,8\cdot1,5\cdot2=1,8\cdot3=5,4\left(m^2\right)\)
Diện tích cửa chớp hình vuông là \(0,5^2=0,25\left(m^2\right)\)
Diện tích cần sơn là:
\(60-5,4-0,25=54,35\left(m^2\right)\)
Số tiền cần phải trả là:
\(54,35\cdot50000=2717500\left(đồng\right)\)

Độ dài đường gấp khúc ABC là 14cm
=>AB+BC=14
mà AB=CD
nên BC+CD=14
Độ dài đường gấp khúc DABC là 20cm
=>DA+AB+BC=20
=>DA+CD+BC=20
=>DA=20-14=6(cm)
mà DA=BC
nên BC=6cm
CD=14-BC=14-6=8(cm)

Hai số chẵn liên tiếp thì hơn kém nhau 2 đơn vị
Số bé là (114-2):2=112:2=56
Số lớn là 56+2=58

\(6=2\cdot3;4=2^2\)
=>\(BCNN\left(6;4\right)=2^2\cdot3=12\)
Gọi số quyển sách là x(quyển)
(Điều kiện: \(x\in Z^+\))
Số quyển sách khi xếp thành mỗi bó 6 quyển hoặc 4 quyển thì vừa đủ nên \(x\in BC\left(6;4\right)\)
=>\(x\in B\left(12\right)\)
mà 35<=x<=40
nên x=36(nhận)
Vậy: Số quyển sách là 36 quyển

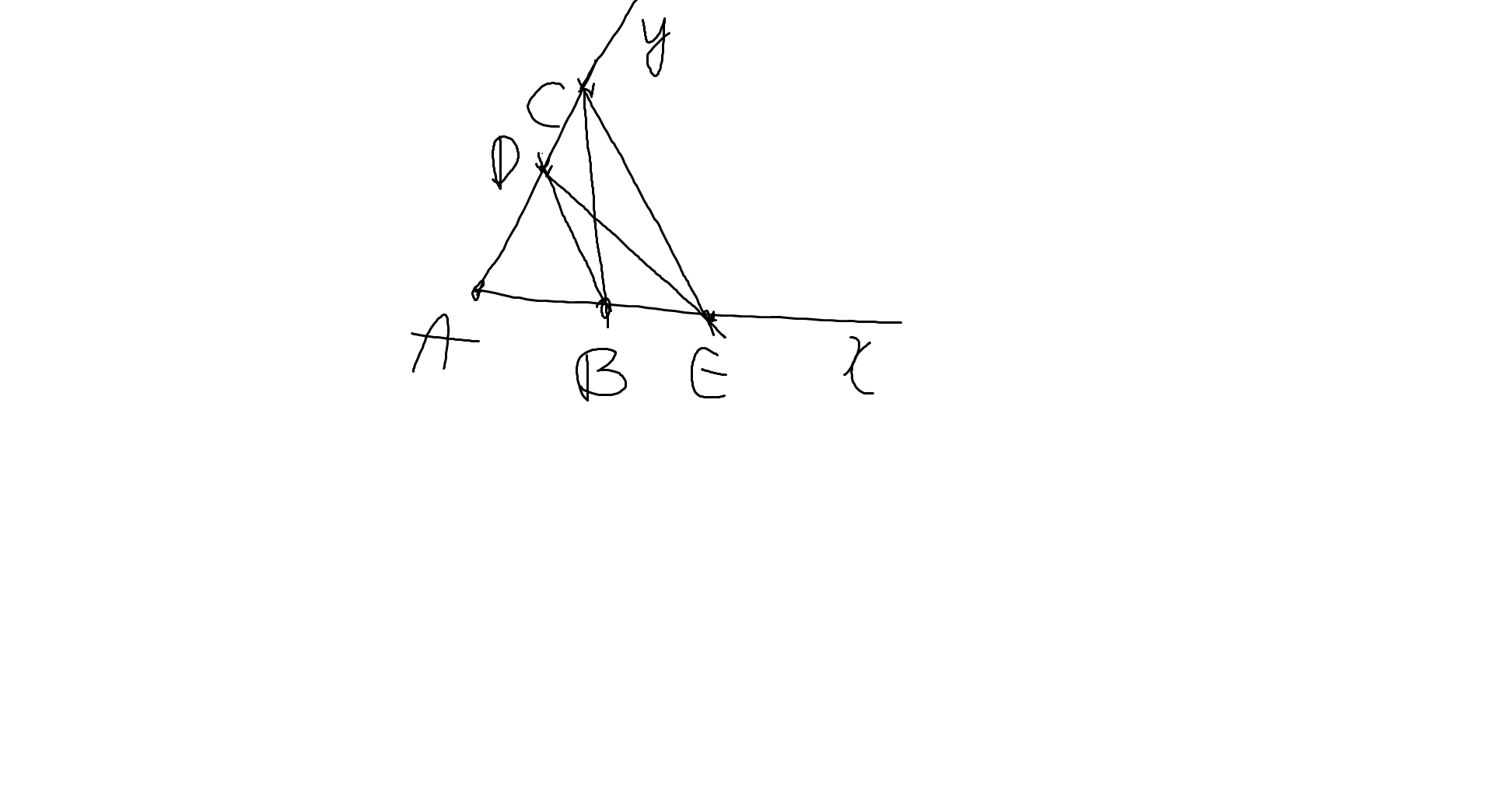





a: Xét (O) có
DB,DE là các tiếp tuyến
Do đó: DB=DE
=>D nằm trên đường trung trực của BE(1)
Ta có: OB=OE
=>O nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra OD là đường trung trực của BE
=>OD\(\perp\)BE tại H
b: Xét ΔDBO vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\left(3\right)\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)DC tại A
Xét ΔDBC vuông tại B có BA là đường cao
nên \(DA\cdot DC=DB^2\left(4\right)\)
Từ (3),(4) suy ra \(DH\cdot DO=DA\cdot DC\)
=>\(\dfrac{DH}{DC}=\dfrac{DA}{DO}\)
Xét ΔDHA và ΔDCO có
\(\dfrac{DH}{DC}=\dfrac{DA}{DO}\)
góc HDA chung
Do đó: ΔDHA~ΔDCO
=>\(\widehat{DHA}=\widehat{DCO}=\widehat{ACB}\)