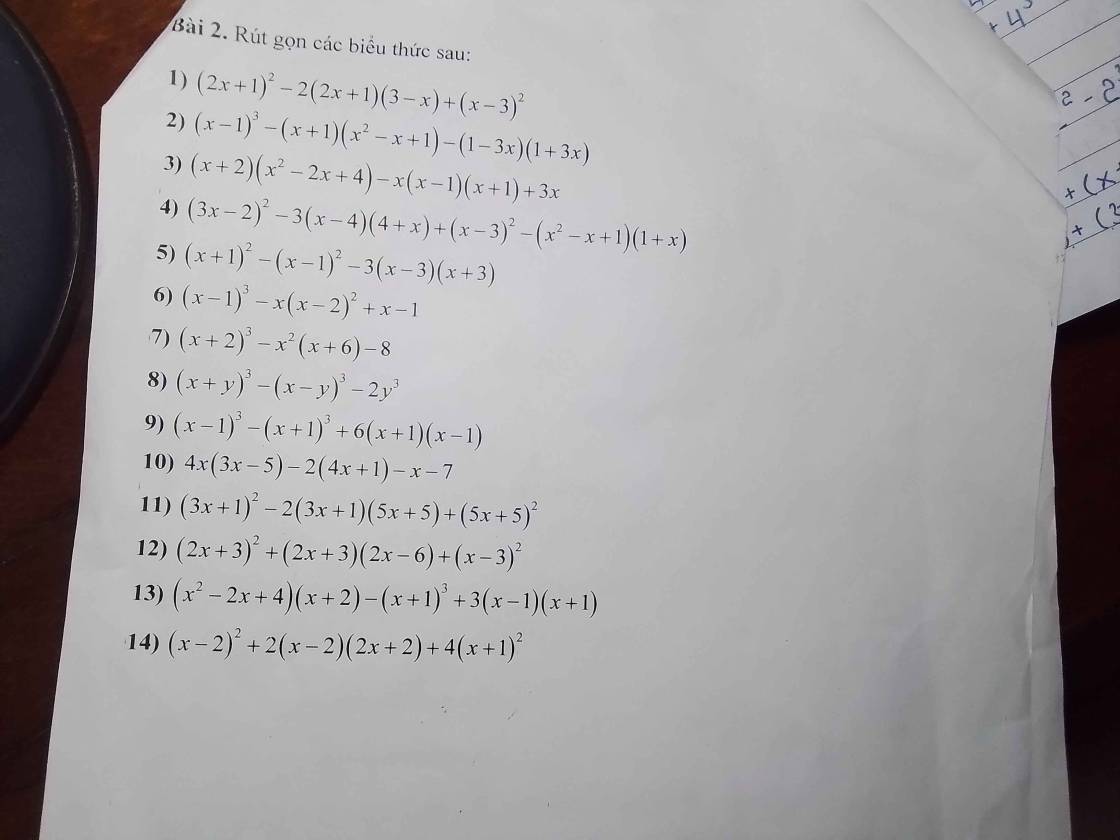1: \(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)

\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)

\(=\left(2x+1+x-3\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)

2: \(\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(1-3x\right)\left(1+3x\right)\)

\(=x^3-3x^2+3x-1-\left(x^3+1\right)-\left(1-9x^2\right)\)

\(=x^3-3x^2+3x-1-x^3-1-1+9x^2\)

\(=6x^2+3x-3\)

3: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-1\right)\left(x+1\right)+3x\)

\(=x^3+8-x\left(x^2-1\right)+3x\)

\(=x^3+8-x^3+x+3x=4x+8\)

4: \(\left(3x-2\right)^2-3\left(x-4\right)\left(x+4\right)+\left(x-3\right)^2-\left(x+1\right)\left(x^2-x+1\right)\)

\(=9x^2-12x+4-3\left(x^2-16\right)+x^2-6x+9-\left(x^3+1\right)\)

\(=10x^2-18x+13-3x^2+48-x^3-1\)

\(=-x^3+7x^2-18x+12\)

5: \(\left(x+1\right)^2-\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)\)

\(=x^2+2x+1-x^2+2x-1-3\left(x^2-9\right)\)

\(=4x-3x^2+27\)

6: \(\left(x-1\right)^3-x\left(x-2\right)^2+x-1\)

\(=x^3-3x^2+3x-1-x\left(x^2-4x+4\right)+x-1\)

\(=x^3-3x^2+4x-2-x^3+4x^2-4x\)

\(=x^2-2\)

7: \(\left(x+2\right)^3-x^2\left(x+6\right)-8\)

\(=x^3+6x^2+12x+8-x^3-6x^2-8\)

=12x

8: \(\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)

\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)

\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)

\(=6x^2y\)

9: \(\left(x-1\right)^3-\left(x+1\right)^3+6\left(x-1\right)\left(x+1\right)\)

\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)

\(=-6x^2-2+6x^2-6=-8\)

10: \(4x\left(3x-5\right)-2\left(4x+1\right)-x-7\)

\(=12x^2-20x-8x-2-x-7\)

\(=12x^2-29x-9\)

11: \(\left(3x+1\right)^2-2\left(3x+1\right)\left(5x+5\right)+\left(5x+5\right)^2\)

\(=\left(5x+5-3x-1\right)^2\)

\(=\left(2x+4\right)^2=4x^2+16x+16\)

12: \(\left(2x+3\right)^2+\left(2x+3\right)\left(2x-6\right)+\left(x-3\right)^2\)

\(=\left(2x+3\right)^2+2\cdot\left(2x+3\right)\left(x-3\right)+\left(x-3\right)^2\)

\(=\left(2x+3+x-3\right)^2=\left(3x\right)^2=9x^2\)

13: \(\left(x^2-2x+4\right)\left(x+2\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)

\(=x^3+8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)

\(=-3x^2-3x+7+3x^2-3=-3x+4\)

14: \(\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+4\left(x+1\right)^2\)

\(=\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+\left(2x+2\right)^2\)

\(=\left(x-2+2x+2\right)^2=\left(3x\right)^2=9x^2\)

Lời giải:
Áp dụng BĐT Cô-si:

$\frac{x^2+y^2}{4}+\frac{1}{x^2+y^2}\geq 2\sqrt{\frac{x^2+y^2}{4}.\frac{1}{x^2+y^2}}=1$

Áp dụng BĐT Bunhiacopxky:

$\frac{3(x^2+y^2)}{4}=\frac{3(1+1)(x^2+y^2)}{8}\geq \frac{3(x+y)^2}{8}=\frac{3.2^2}{8}=\frac{3}{2}$

$\Rightarrow B\geq 1+\frac{3}{2}=\frac{5}{2}$

Vậy $B_{\min}=\frac{5}{2}$

Giá trị này đạt tại $x=y=1$

Xét tam giác AEB và tam giác CFD ta có 

AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt) 

Vậy tam giác AEB = tam giác CFD ( c.g.c ) 

=> AE = FC ( 2 cạnh tương ứng ) (1)

tương tự với tam giác AFD = tam giác EBC 

=> AF = EC (2) 

Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF 

Xét tam giác AEB và tam giác CFD ta có 

AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt) 

Vậy tam giác AEB = tam giác CFD ( c.g.c ) 

=> AE = FC ( 2 cạnh tương ứng ) (1)

tương tự với tam giác AFD = tam giác EBC 

=> AF = EC (2) 

Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF 

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

ΔABC~ΔHBA

=>\(\dfrac{AB}{HB}=\dfrac{BC}{BA}=\dfrac{AC}{HA}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)

c: Xét ΔAHB có AD là phân giác

nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)(1)

Xét ΔCHA vuông tại H và ΔCAB vuông tại A có

\(\widehat{HCA}\) chung

Do đó: ΔCHA~ΔCAB

=>\(\dfrac{CH}{CA}=\dfrac{AH}{AB}\)(2)

Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{CAB}=90^0\)

\(\widehat{CDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)

mà \(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác của góc BAH)

nên \(\widehat{CAD}=\widehat{CDA}\)

=>CA=CD(3)

Từ (1),(2),(3) suy ra \(\dfrac{DH}{DB}=\dfrac{HC}{DC}\)

=>\(DH\cdot DC=HC\cdot DB\)

Lời giải:

Đổi 30p = 0,5 giờ

Thời gian xe đi: $\frac{AB}{40}$ (h) 

Thời gian xe về: $\frac{AB}{45}$ (h) 

Theo bài ra ta có: $\frac{AB}{40}-\frac{AB}{45}=0,5$

$\Leftrightarrow AB.\frac{1}{360}=0,5$

$\Leftrightarrow AB=0,5: \frac{1}{360}=180$ (km)

 Gọi \(P_i\) là biến cố: "Rút được tấm thẻ ghi số \(i\)." với \(5\le i\le8\)

 Theo đề bài, ta có: \(P_7=3P_4;P_5=4P_7;P_5=2P_8\). Khi đó \(P_5=12P_4,P_8=6P_4\)

 Vì \(P_4\cup P_5\cup P_7\cup P_8=\Omega\) và \(P_5,P_6,P_7,P_8\) độc lập từng đôi nên \(P_4+P_5+P_7+P_8=1\)

 Do đó \(P_4+12P_4+2P_4+6P_4=1\) \(\Leftrightarrow P_4=\dfrac{1}{21}\)

 \(\Rightarrow P_5=\dfrac{12}{21};P_8=\dfrac{6}{21}\)

 \(\Rightarrow P=P_5+P_8=\dfrac{18}{21}=\dfrac{6}{7}\) (P là xác suất cần tìm)

\(M=-x^4+y^4+x^3-x^2y+xy^2-y^3\)

\(=-\left(x^2-y^2\right)\left(x^2+y^2\right)+x^2\left(x-y\right)+y^2\left(x-y\right)\)

\(=-\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)+\left(x-y\right)\left(x^2+y^2\right)\)

\(=\left(x-y\right)\left(x^2+y^2\right)\left[-\left(x+y\right)+1\right]\)

\(=\left(x-y\right)\left(x^2+y^2\right)\left(-1+1\right)=0\)

a: |2x-1|=3

=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=2\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

Thay x=-1 vào A, ta được:

\(A=\dfrac{-1+2}{\left(-1\right)^2-4\cdot\left(-1\right)+4}=\dfrac{1}{1+4+4}=\dfrac{1}{9}\)

b: P=A:B

\(=\dfrac{x+2}{\left(x-2\right)^2}:\left(\dfrac{x+2}{x}+\dfrac{1}{x-2}+\dfrac{6-x^2}{x\left(x-2\right)}\right)\)

\(=\dfrac{x+2}{\left(x-2\right)^2}:\dfrac{\left(x+2\right)\left(x-2\right)+x+6-x^2}{x\left(x-2\right)}\)

\(=\dfrac{x+2}{\left(x-2\right)^2}\cdot\dfrac{x\left(x-2\right)}{x^2-4+x+6-x^2}\)

\(=\dfrac{x+2}{x-2}\cdot\dfrac{x}{x+2}=\dfrac{x}{x-2}\)

c: P<1

=>P-1<0

=>\(\dfrac{x-x+2}{x-2}< 0\)

=>\(\dfrac{2}{x-2}< 0\)

=>x-2<0

=>x<2

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 2\\x\notin\left\{0;-2\right\}\end{matrix}\right.\)

Lời giải:

a. Áp dụng định lý Pitago:

$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8$ 

$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ 

b.

Xét tam giác $AEH$ và $AHB$ có:

$\widehat{A}$ chung

$\widehat{AEH}=\widehat{AHB}=90^0$

$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)

$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$

$\Rightarrow AH^2=AE.AB(1)$
Hoàn toàn tương tự: $\triangle AFH\sim \triangle AHC$

$\Rightarrow AH^2=AF.AC(2)$

Từ $(1); (2)\Rightarrow AE.AB=AF.AC$

c.

$HE\perp AB, AB\perp AC$ nên $HE\parallel AC$

Tam giác vuông $BEH$ vuông tại $E$ có trung tuyến $EM$ ứng với cạnh huyền $BH$

nên $EM=\frac{BH}{2}=MH$

$\Rightarrow EMH$ cân tại $M$

$\Rightarrow \widehat{MEH}=\widehat{MHE}=\widehat{HCA}(3)$ (2 góc đồng vị)

Tứ giác $AEHF$ có 3 góc $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hcn. 

$\Rightarrow \widehat{HEF}=\widehat{HAF}=\widehat{HAC}(4)$

Từ $(3); (4)\Rightarrow \widehat{MEH}+\widehat{HEF}=\widehat{HCA}+\widehat{HAC}$

$\Rightarrow \widehat{MEF}=\widehat{HCA}+\widehat{HAC}=90^0$

$\Rightarrow EM\perp EF$

Hình vẽ:

a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có

\(\widehat{IAB}\) chung

Do đó: ΔAIB~ΔAEC

=>\(\dfrac{AI}{AE}=\dfrac{AB}{AC}\)

=>\(AI\cdot AC=AB\cdot AE\)

b: Xét ΔCBI vuông tại I và ΔACF vuông tại F có

\(\widehat{BCI}=\widehat{CAF}\)(BC//AF)

Do đó; ΔCBI~ΔACF

=>\(\dfrac{CI}{AF}=\dfrac{CB}{AC}\)

=>\(CB\cdot AF=CI\cdot AC\)

\(AB\cdot AE+CB\cdot AF\)

\(=AI\cdot AC+CI\cdot AC\)

\(=AC\left(AI+CI\right)=AC^2\)

c: Xét tứ giác AECF có \(\widehat{AEC}+\widehat{AFC}=90^0+90^0=180^0\)

nên AECF là tứ giác nội tiếp

=>\(\widehat{FAC}=\widehat{FEC}\)

mà \(\widehat{FAC}=\widehat{BCA}\)(AD//BC)

nên \(\widehat{CEF}=\widehat{BCA}\)