 giúp e câu 2b ạ.
giúp e câu 2b ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
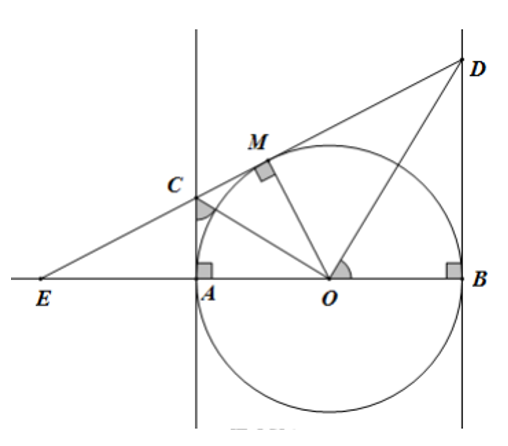
Vì AC là tiếp tuyến của (O) nên OA ⊥ AC => ˆOAC = 90o���^ = 90�
Vì MC là tiếp tuyến của (O) nên OM ⊥ MC => ˆOMC = 90o���^ = 90�
=> ˆOAC +ˆOMC =180o.���^ +���^ =180�. Suy ra OACM là tứ giác nội tiếp

1: Xét tứ giác BMNC có \(\widehat{BMC}=\widehat{BNC}=90^0\)
nên BMNC là tứ giác nội tiếp
=>B,M,N,C cùng thuộc một đường tròn
2:
Kẻ tiếp tuyến Ax của (O)
=>Ax\(\perp\)OA tại A
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{ANM}\left(=180^0-\widehat{MNC}\right)\)
nên \(\widehat{xAC}=\widehat{ANM}\)
=>Ax//MN
=>OA\(\perp\)MN
mà MN\(\perp\)NK
nên NK//OA

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là các đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
Xét tứ giác HECF có \(\widehat{HEC}+\widehat{HFC}=90^0+90^0=180^0\)
nên HECF là tứ giác nội tiếp
=>\(\widehat{HEF}=\widehat{HCF}\)
b: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp
=>\(\widehat{DEH}=\widehat{DAH}\)
mà \(\widehat{HEF}=\widehat{HCF}\)
và \(\widehat{DAH}=\widehat{HCF}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEB}=\widehat{FEB}\)
=>EB là phân giác của góc DEF

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{3}{4x}-\dfrac{2}{5y}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{6}{4x}-\dfrac{4}{5y}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{6}{4x}=7+6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{3}{2x}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}\left(\dfrac{2}{3}+\dfrac{3}{2}\right)=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}\cdot\dfrac{13}{6}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=13:\dfrac{13}{6}=6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{3x}=7-\dfrac{2}{3\cdot\dfrac{1}{6}}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{\dfrac{1}{2}}=7-2\cdot2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\5y=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{4}{15}\end{matrix}\right.\left(nhận\right)\)

M = x + 2 - √(x² - 2x + 1)
= x + 2 - √(x - 1)²
= x + 2 - |x - 1| (1)
Với x ≥ 1, ta có:
(1) = x + 2 - x + 1
= 3
Với x < 1, ta có:
M = x + 2 - 1 + x
= 2x + 1

Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

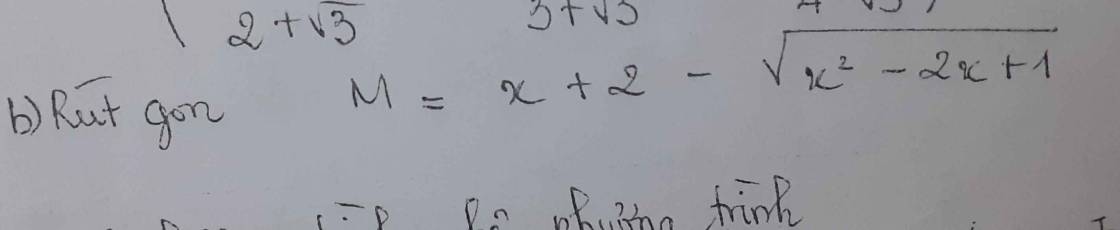
Thế x = -1 vào (P), ta có:
y = (-1)² = 1
⇒ A(-1; 1)
Thế x = 2 vào (P), ta có:
y = 2² = 4
⇒ B(2; 4)
Gọi (d): y = ax + b (a ≠ 0) là phương trình đường thẳng AB
Thế tọa độ điểm A(-1; 1) vào (d), ta có:
a.(-1) + b = 1
⇔ -a + b = 1
⇔ b = 1 + a (1)
Thế tọa độ điểm B(2; 4) vào (d), ta có:
a.2 + b = 4
⇔ 2a + b = 4 (2)
Thế (1) vào (2), ta có:
2a + 1 + a = 4
⇔ 3a = 4 - 1
⇔ 3a = 3
⇔ a = 3 : 3
⇔ a = 1 (nhận)
Thế a = 1 vào (1), ta có:
b = 1 + 1 = 2
⇒ (d): y = x + 2
Ta có:
OA² = 1 + 1 = 2
⇒ OA = √2
AB² = 3² + 3² = 18
⇒ AB = 3√2
OB² = 2² + 4² = 20
⇒ OB = 2√5
∆OAB có:
OB² = OA² + AB² = 20
⇒ ∆OAB vuông tại A (định lý Pythagore đảo)
Diện tích ∆OAB:
S = √2.3√2 : 2 = 3 (đvdt)