1=5 +5-2+16=16-28+100+1=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B D E K O C d1 d2 H I G
a/
\(d_1;d_2\) là tiếp tuyến với đường tròn tại A và B \(\Rightarrow d_1\perp AB;d_2\perp AB\) => \(d_1\)//\(d_2\)
Xét tg vuông ABK có
\(\widehat{ACB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AK^2=KC.KB\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
b/
Ta có
DA=DC (2 tiếp tuyến của 1 đường tròn cùng xuất phát từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau) (1)
EC=EB (lý do như trên) => tg EBC cân tại E\(\Rightarrow\widehat{ECB}=\widehat{KBE}\) (2 góc ở đáy của tg cân) (*)
\(\widehat{KBE}=\widehat{AKB}\) (góc so le trong) (**)
\(\widehat{KCD}=\widehat{ECB}\) (Góc đối đỉnh) (***)
Từ (*) (**) và (***) \(\Rightarrow\widehat{AKB}=\widehat{KCD}\) => tg DCK cân tại D => DC=DK (2)
Từ (1) và (2) => DA=DK nên K là trung điểm của AK
c/ Gọi I là giao của CH với BD
Ta có
\(CH\perp AB;d_1\perp AB\) => CH//\(d_1\)
\(\Rightarrow\frac{IC}{DK}=\frac{BC}{BK}=\frac{BH}{BA}=\frac{IH}{DA}\) (Talet trong tam giác)
Mà DK=DA => IC=IH => BD đi qua trung điểm I của CH
d/
câu a ý số 2 bạn còn cách nào khác ko? Tại mk chx hc góc nội tiếp chắn nửa đường tròn

B=\(\frac{x-2\sqrt{x}+1}{x-1}\) =\(\frac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)=\(\frac{\sqrt{x}-1}{\sqrt{x}+1}\)

A B C D
B: Là vị trí thuyền hiện tại
D: là vị trí thuyền sau 10 phút
AC: chiều cao ngọn hải đăng = 63 m
Xét tg vuông ABC
\(\tan\widehat{ABC}=\tan19^o=\frac{AC}{AB}=\frac{63}{AB}\Rightarrow AB=\frac{63}{\tan19^o}\)
Xét tg vuông ACD có
\(\tan\widehat{ADC}=\tan54^o=\frac{AC}{AD}=\frac{63}{AD}\Rightarrow AD=\frac{63}{\tan54^o}\)
Quãng đường thuyền đi được sau 10' là
\(BD=AB-AD=\frac{63}{\tan19^o}-\frac{63}{\tan54^o}\)

a) \(y=m\left(2x-1\right)+3-2x,\forall m\)
\(\Leftrightarrow m\left(2x-1\right)+3-2x-y=0,\forall m\)
\(\Leftrightarrow\hept{\begin{cases}2x-1=0\\3-2x-y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=2\end{cases}}\)
Vậy khi \(m\)thay đổi đường thẳng \(\left(d\right)\)luôn đi qua điểm có tọa độ \(\left(\frac{1}{2},2\right)\).
b) \(y=m\left(2x-1\right)+3-2x=\left(2m-2\right)x+3-m\)
\(\Leftrightarrow y-\left(2m-2\right)x+m-3=0\)
Khoảng cách từ điểm \(O\left(0,0\right)\)đến đường thẳng \(d\)là:
\(d=\frac{\left|m-3\right|}{\sqrt{\left(2m-2\right)^2+1^2}}\Leftrightarrow d^2\left(4m^2-8m+5\right)=m^2-6m+9\)
\(\Leftrightarrow m^2\left(4d^2-1\right)-2m\left(4d^2-3\right)+5d^2-9=0\)(1)
Với \(m=0\): \(d=\frac{3\sqrt{5}}{5}\).
Với \(m\ne0\)ta coi \(m\)là phương trình bậc \(2\)ẩn \(m\)tham số \(d\).
Để phương trình có nghiệm thì
\(\Delta'\ge0\Leftrightarrow\left(4d^2-3\right)^2-\left(5d^2-9\right)\left(4d^2-1\right)\ge0\)
\(\Leftrightarrow17d^2-4d^4\ge0\)
\(\Leftrightarrow\frac{-\sqrt{17}}{2}\le d\le\frac{\sqrt{17}}{2}\).
Vây GTLN cần tìm là \(d=\frac{\sqrt{17}}{2}\).

ĐKXĐ : \(x\ge\frac{1}{2}\)
=> \(2+\sqrt{2x-1}=x\)
<=> \(\sqrt{2x-1}=x-2\)
<=> \(\left(\sqrt{2x-1}\right)^2=\left(x-2\right)^2\)
<=> 2x - 1 = x2 - 4x + 4
<=> x2 - 6x + 5 = 0
<=> (x - 1)(x - 5) = 0
<=> \(\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
Xyz thay x = 1 vô thì không xảy ra đẳng thức đâu
ĐK : x >= 2 còn lại làm như bạn

ta có :
\(\left(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\right)^2=4+\sqrt{7}+4-\sqrt{7}-2\sqrt{4+\sqrt{7}}.\sqrt{4-\sqrt{7}}\)
\(=8-2\sqrt{16-7}=8-2\sqrt{9}=2\)
vậy \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}=\sqrt{2}\)

\(\sqrt{4-\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\cdot\left(\sqrt{10}-\sqrt{6}\right)=\left(4+\sqrt{15}\right)\sqrt{8-2\sqrt{15}.}\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2=2\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)=2>\sqrt{3}\)
vậy số bên trái lơn hơn \(\sqrt{3}\)
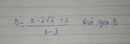
đầu bài kiểu gì đây:))?
Tk cho bn để chuộc lỗi