Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


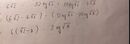

a) \(\sqrt{144}-\sqrt{9}-\sqrt{250}\cdot\sqrt{1,6}=12-3-20=-11\)
a) \(\frac{\sqrt{144}}{\sqrt{9}}-\sqrt{250}.\sqrt{1,6}\) = \(\frac{12}{3}-\sqrt{250.1,6}\) = \(4-\sqrt{25.16}\) = \(4-20=-16\)
b) \(\frac{\sqrt{3,6}}{\sqrt{4,9}}-\sqrt{3.2^3.24}\) = \(\sqrt{\frac{36}{49}}-\sqrt{576}\) = \(\frac{6}{7}-24=-\frac{162}{7}\)
c) \(\sqrt{2+\sqrt{3}}\) = \(\sqrt{3+2.\frac{\sqrt{3}}{2}+\frac{1}{4}-\frac{3}{4}}\) = \(\sqrt{\left(\sqrt{3}+\frac{1}{2}\right)^2-\left(\frac{\sqrt{3}}{2}\right)^2}\)
= \(\sqrt{\left(\sqrt{3}+\frac{1}{2}-\frac{\sqrt{3}}{2}\right)\left(\sqrt{3}+\frac{1}{2}+\frac{\sqrt{3}}{2}\right)}\)


b/ B=(cosa−sina)2+(cosa+sina)2+cos4a−sin4a−2cos2aB=(cosa−sina)2+(cosa+sina)2+cos4a−sin4a−2cos2a
=cos2a−2cosa.sina+sin2a+cos2a+2cosa.sina+sin2a+(cos2a+sin2a)(cos2a−sin2a)−2cos2a=cos2a−2cosa.sina+sin2a+cos2a+2cosa.sina+sin2a+(cos2a+sin2a)(cos2a−sin2a)−2cos2a
=2+(cos2a−sin2a)−2cos2a=2+(cos2a−sin2a)−2cos2a
=2−sin2a−cos2a=2−1=1