giải giúp em với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x^2+4+6}{5-6x}< 0\)
Nhận xét:
\(x^2\ge0,\forall x\)
\(\Rightarrow x^2+4+6\ge10,\forall x\)
Do đó \(\dfrac{x^2+4+6}{5-6x}< 0\) khi và chỉ khi:
\(5-6x< 0\)
\(\Leftrightarrow6x>5\)
\(\Leftrightarrow x>\dfrac{5}{6}\)
Vậy \(x>\dfrac{5}{6}\)

\(\sqrt{x}=1-\sqrt{3}\)
Nhận xét:
\(\sqrt{3}>\sqrt{1}=1\)
\(\Rightarrow1-\sqrt{3}< 0\)
\(\Rightarrow\sqrt{x}< 0\) (vô lí)
Vậy không tìm được giá trị x thoả mãn đề bài

\(\left(a+1\right)\left(a+2\right)\left(a+3\right)\left(a+4\right)+1\\ =\left[\left(a+1\right)\left(a+4\right)\right]\left[\left(a+2\right)\left(a+3\right)\right]+1\\ =\left(a^2+5a+4\right)\left(a^2+5a+6\right)+1\\ =\left(a^2+5a+4\right)\left(a^2+5a+4\right)+2\left(a^2+5a+4\right)+1\\ \left(a^2+5a+4\right)^2+2\left(a^2+5a+4\right)+1\\ =\left(a^2+5a+5\right)^2\)

a) $-(2x-4)(x+2)+(x+2)^2+(x-2)^2-4x^2-1-4x=-3$
$\Leftrightarrow (x-2)^2-2(x-2)(x+2)+(x+2)^2-4x^2-4x+2=0$
$\Leftrightarrow (x-2+x+2)^2-4x^2-4x+2=0$
$\Leftrightarrow (2x)^2-4x^2-4x=-2$
$\Leftrightarrow -4x=-2$
$\Leftrightarrow x=\frac12$
b) $(4x-1)^2-16(x+1)(x+3)=25$
$\Leftrightarrow (4x)^2-2.4x.1+1^2-16(x^2+4x+3)=25$
$\Leftrightarrow 16x^2-8x+1-16x^2-64x-48=25$
$\Leftrightarrow -72x-47=25$
$\Leftrightarrow -72x=72$
$\Leftrightarrow x=-1$
c) $(3x-7)^2=9(3x-7)(x+5)+694$
$\Leftrightarrow (3x)^2-2.3x.7+7^2=9(3x^2+8x-35)+694$
$\Leftrightarrow 9x^2-42x+49=27x^2+72x-315+694$
$\Leftrightarrow 18x^2+114x+330=0$
$\Leftrightarrow 9x^2+57x+165=0$
$\Leftrightarrow 9\left(x+\frac{19}{6}\right)^2+\frac{299}{4}=0$ (vô lí)
=> Pt vô nghiệm
d) $(2x-1)^2+(x+3)^2=5(x+7)(x-7)-3x$
$\Leftrightarrow 4x^2-4x+1+x^2+6x+9=5(x^2-49)-3x$
$\Leftrightarrow 5x^2+2x+10=5x^2-3x-245$
$\Leftrightarrow 5x=-255$
$\Leftrightarrow x=-51$
#$\mathtt{Toru}$

a: \(-\left(2x-4\right)\left(x+2\right)+\left(x+2\right)^2+\left(x-2\right)^2-4x^2-1-4x=-3\)
=>\(-2\left(x^2-4\right)+x^2+4x+4+x^2-4x+4-4x^2-1-4x=-3\)
=>\(-2x^2+8-2x^2-4x+7+3=0\)
=>\(-4x^2-4x+18=0\)
=>\(x=\dfrac{-1\pm\sqrt{19}}{2}\)
b: \(\left(4x-1\right)^2-16\left(x+1\right)\left(x+3\right)=25\)
=>\(16x^2-8x+1-16\left(x^2+4x+3\right)-25=0\)
=>\(16x^2-8x-24-16x^2-64x-48=0\)
=>-72x-72=0
=>x=-1
c: \(\left(3x-7\right)^2=9\left(3x-7\right)\left(x+5\right)+694\)
=>\(9\left(3x^2+15x-7x-35\right)+694=9x^2-42x+49\)
=>\(27x^2+72x-315+694-9x^2+42x-49=0\)
=>\(18x^2+114x+330=0\)
=>\(x\in\varnothing\)
d: \(\left(2x-1\right)^2+\left(x+3\right)^2=5\left(x+7\right)\left(x-7\right)-3x\)
=>\(4x^2-4x+1+x^2+6x+9=5\left(x^2-49\right)-3x\)
=>\(5x^2+2x+10-5x^2+245+3x=0\)
=>5x+255=0
=>x+51=0
=>x=-51

Bài 7
1)
\(A=8\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =3^{32}-1\)
2)
\(B=\left(1-3\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =-\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =-\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =-\left(3^{32}-1\right)\\ =1-3^{32}\)
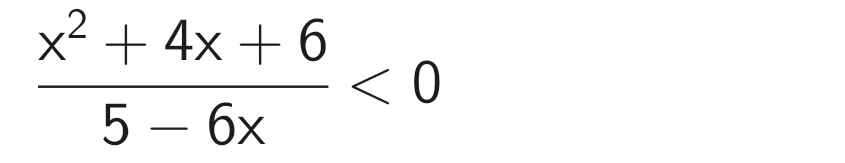
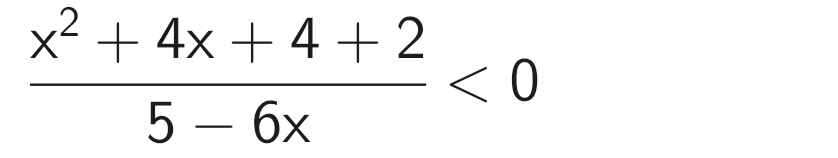
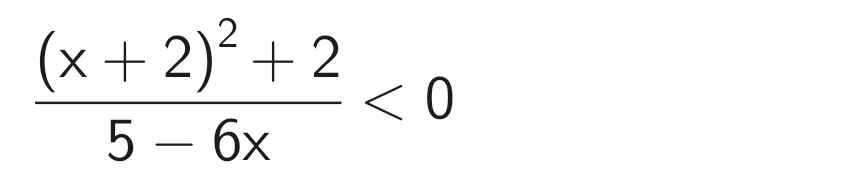

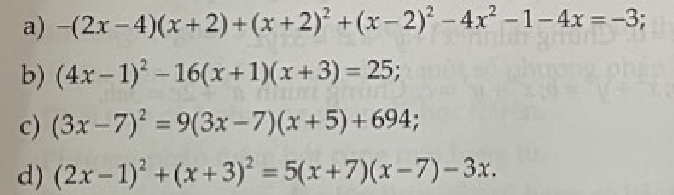
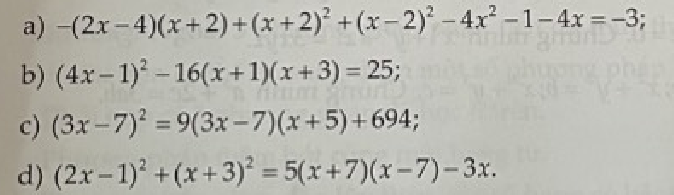

a: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
=>\(DB=\sqrt{5^2-4^2}=3\left(cm\right)\)
b: Xét ΔHDB vuông tại D và ΔHEA vuông tại E có
\(\widehat{DHB}=\widehat{EHA}\)(hai góc đối đỉnh)
Do đó: ΔHDB~ΔHEA
=>\(\dfrac{HD}{HE}=\dfrac{HB}{HA}\)
=>\(HD\cdot HA=HB\cdot HE\)