 Anh chị giúp em với có được không ạ?
Anh chị giúp em với có được không ạ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\frac{1}{49}+\frac{2}{48}+\frac{3}{47}+...+\frac{48}{2}+49\)
\(=\left(\frac{1}{49}+1\right)+\left(\frac{2}{48}+1\right)+...+\left(\frac{48}{2}+1\right)+1\)
\(=\left(\frac{50}{49}+\frac{50}{48}+...+\frac{50}{2}\right)+1\)
\(=\frac{50}{50}+\frac{50}{49}+\frac{50}{48}+...\frac{50}{2}\)
\(=50.\left(\frac{1}{50}+\frac{1}{49}+...\frac{1}{2}\right)\)
\(\Rightarrow\frac{S}{P}=\frac{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{50}}{50.\left(\frac{1}{50}+\frac{1}{49}+\frac{1}{48}+...+\frac{1}{2}\right)}\)
\(\Rightarrow\frac{S}{P}=\frac{1}{50}\)
<br class="Apple-interchange-newline"><div></div>P=149 +248 +347 +...+482 +49
=(149 +1)+(248 +1)+...+(482 +1)+1
=(5049 +5048 +...+502 )+1
=5050 +5049 +5048 +...502
=50.(150 +149 +...12 )

\(\frac{2}{5}-\frac{x}{7}=\frac{1}{4}+\frac{2}{-9}=\frac{-1}{36}\)
\(\frac{x}{7}=\frac{2}{5}-\frac{-1}{36}=\frac{2}{5}+\frac{1}{36}=\frac{67}{180}\)
#Monster

\(K=\frac{4}{2.4}+\frac{4}{4.6}+\frac{4}{6.8}+...+\frac{4}{2008.2010}\)
\(=2\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+..+\frac{1}{2008}-\frac{1}{2010}\right)\)
\(=2.\left(\frac{1}{2}-\frac{1}{2010}\right)=2\left(\frac{2019}{4020}\right)=\frac{673}{670}\)

Ta có \(\frac{1}{10.11}=\frac{1}{10}-\frac{1}{11}\)
... \(\frac{1}{69.70}=\frac{1}{69}-\frac{1}{70}\)
Vì vậy
\(A=7\left(\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}+..+\frac{1}{69}-\frac{1}{70}\right)=7\left(\frac{1}{10}-\frac{1}{70}\right)=\frac{3}{5}\)

a)
⇒
b)Ta có:
⇒
⇒ON là tia phân giác của

\(\frac{7}{-25}+\frac{-18}{25}+\frac{4}{23}+\frac{5}{7}+\frac{19}{23}\)
\(=\left(-\frac{7}{25}-\frac{18}{25}\right)+\left(\frac{4}{23}+\frac{19}{23}\right)+\frac{5}{7}\)
\(=-1+1+\frac{5}{7}\)
\(=0+\frac{5}{7}\)
\(=\frac{5}{7}\)
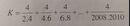
hơi dài á
a, ta có:
kẻ đường cao CH
=> SABC \(=\frac{CHxAB}{2}\) ; SCDB \(=\frac{BDxCH}{2}\)
mà BD= \(\frac{1}{4}\)AB nên SCDB=\(\frac{1}{4}\)xSABC
CMTT với SBEC = \(\frac{1}{4}\)xSABC
b, ta có: SCDB = SBEC = \(\frac{1}{4}\)xSABC
=> SDBG+SBGC = SBGC+SEGC
=> SDBG=SEGC