\(\left|x-2\right|=12\\ =>\left[{}\begin{matrix}x-2=12\\x-2=-12\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=12+2=14\left(ktm\right)\\x=-12+2=-10\left(tm\right)\end{matrix}\right.\\ \left|y+1\right|=2025\\ =>\left[{}\begin{matrix}y+1=2025\\y+1=-2025\end{matrix}\right.\\ =>\left[{}\begin{matrix}y=2025-1=2024\left(tm\right)\\y=-2025-1=-2026\left(ktm\right)\end{matrix}\right.\)

\(A=202x+y-4=202\cdot-10+2024-4=-2020+2024-4=0\)

trả lời xong nhớ cho coin

ko bế ơi

like thôi

a) \(\dfrac{x}{3}+\dfrac{1}{y}=-\dfrac{5}{6}\) (ĐK: \(y\ne0;x,y\in\mathbb{Z}\))

\(\Rightarrow x+\dfrac{3}{y}=-\dfrac{5}{2}\)

\(\Rightarrow x=-\dfrac{5}{2}-\dfrac{3}{y}\)

\(\Rightarrow2x=-5-\dfrac{6}{y}\)

Vì x nguyên nên \(-\dfrac{6}{y}\) nguyên \(\Rightarrow-6⋮y\)

\(\Rightarrow y\inƯ\left(-6\right)\)

Ta có bảng:

Và x, y tìm được đều tmdk. Vậy:...

b) \(\dfrac{5}{3}< \dfrac{x}{y}< \dfrac{15}{4}\) (1) (ĐK: \(y\ne0;x,y\in\mathbb{Z}\))

+, Với y > 0 thì (1) trở thành: 

\(\dfrac{5}{3}y< x< \dfrac{15}{4}y\\ \Rightarrow\dfrac{10}{3}y< 2x< \dfrac{15}{2}y\\ \Rightarrow\dfrac{10}{3}y-3y< 2x-3y< \dfrac{15}{2}y-3y\\ \Rightarrow\dfrac{1}{3}y< 5< \dfrac{9}{2}y\\ \Rightarrow\dfrac{10}{9}< y< 15\\ \Rightarrow y\in\left\{1;2;3;...;14\right\}\left(\text{vì }y\in\mathbb{Z}\right)\)

Tới đây thay lần lượt các giá trị của y vào 2x-3y=5 để tìm x nhé.

+, Với y < 0 thì (1) trở thành:

\(\dfrac{15}{4}y< x< \dfrac{5}{3}y\). Sau đó bạn làm tương tự như trường hợp trên là được.

#$\mathtt{Toru}$

f(1)=g(2)

=>\(2\cdot1^2+a\cdot1+4=2^2-5\cdot2+b\)

=>a+6=b-6

=>a=b-12

f(-1)=g(5)

=>\(2\cdot\left(-1\right)^2+a\cdot\left(-1\right)+4=5^2-5\cdot5+b\)

=>-a+4+2=b

=>-a+6=b

=>-b+12+6=b

=>-2b=-18

=>b=9

=>a=9-12=-3

thay x = 1 vào f(x), có

f(1) =2.1² + 1a + 4

f(1) =2 + a + 4

f(1) =a + 6

=> f(6) =a + 6

thay x = 2 vào g(x) , có

g(2) =2² - 5.2 + b

g(2) =4 - 10 + b

g(2) =-6 + b

=> g(2) = -6 + b

thay x = -1 vào f(x), có

f(-1) =2.(-1)² - 1a + 4

f(-1) = 2 + a + 4

f(-1) = 6 + a

=> f(-1) = 6 + a

thay x = 5 vào g(x) , có

g(5) =(5)² - 5.(5) + b

g(5) = 25 - 25 + b

g(5) = + b

vậy g(5)= b

có f(1) = g(2)

=> a + 6 = -6 + b

=> a + b = 0

=> a = -b hoặc b = -a

có f(-1) = g(5)

=> 6 + a = b

=> 6 = b - a

=> 6 = b - (-b)

=> 6 = b + b

=> b = 3 

=> a = -b = -3

\(a)4\left(x+2\right)-\left(5x+1\right)=3x-1\\ =>4x+8-5x-1=3x-1\\ =>-x+7=3x-1\\ =>3x+1=7+1\\ =>4x=8\\ =>x=\dfrac{8}{4}=2\\ b)2\left(5x-2\right)-3\left(x-1\right)=x+2\\ =>10x-4-3x+3=x+2\\ =>7x-1=x+2\\ =>7x-x=2+1\\ =>6x=3\\ =>x=\dfrac{3}{6}=\dfrac{1}{2}\)

\(4.\left(x+2\right)-\left(5x+1\right)=3x-1\\ \Rightarrow4x+8-5x-1=3x-1\\ \Rightarrow-x+7=3x-1\\ \Rightarrow3x+x=7+1\\ \Rightarrow4x=8\\ \Rightarrow x=2\)
Vậy...

\(2.\left(5x-2\right)-3.\left(x-1\right)=x+2\\ \Rightarrow10x-4-3x+1=x+2\\ \Rightarrow7x-3 =x+2\\ \Rightarrow7x-x=2+3\\\Rightarrow6x=5\\ \Rightarrow x=\dfrac{5}{6}\)
Vậy...

\(50+\dfrac{50}{3}+\dfrac{25}{3}+\dfrac{20}{4}+...+\dfrac{100}{98\cdot99}+\dfrac{1}{99}\)

\(=\dfrac{100}{2}+\dfrac{100}{6}+\dfrac{100}{12}+...+\dfrac{100}{98\cdot99}+\dfrac{100}{99\cdot100}\)

\(=100\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=100\cdot\dfrac{99}{100}=99\)

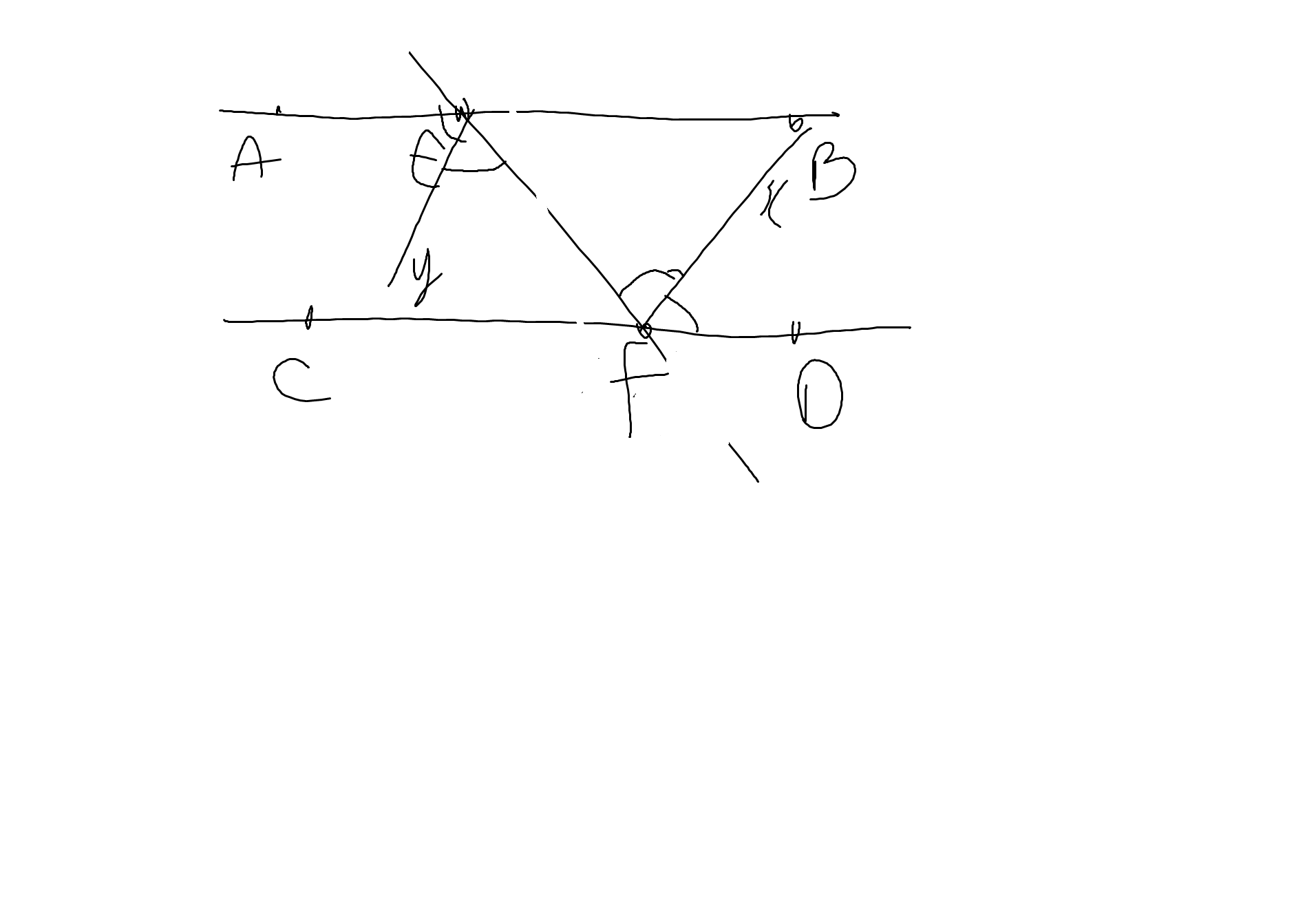
Gọi hai góc so le trong là \(\widehat{AEF};\widehat{EFD}\); Ey;Fx lần lượt là phân giác của góc AEF;góc EFD

Vì AB//CD nên \(\widehat{AEF}=\widehat{EFD}\)(hai góc so le trong)

mà \(\widehat{yEF}=\dfrac{\widehat{AEF}}{2};\widehat{xFE}=\dfrac{\widehat{EFD}}{2}\)

nên \(\widehat{yEF}=\widehat{xFE}\)

mà hai góc này là hai góc ở vị trí so le trong

nên Ey//Fx

a) TH1: x = 1 

=> Giá tiền phải trả là: 11000 (đồng) 

TH2: x > 1 

=> Giá tiền phải trả là:

11000 + 10000(x - 1) 

= 11000 + 10000x - 10000 

= 10000x + 1000 (đồng) (1) 

b) Người đó đi 50km ta thay x = 50 vào (1) ta có:

10000*50 + 1000 

= 500000 + 1000 

= 501000 (đồng)