Giúp e tìm công thức tổng quát với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\lim n^2\left(-4+\dfrac{1}{\sqrt{n}}-\dfrac{2}{n^2}\right)\)
Do \(\lim n^2=+\infty\)
\(\lim\left(-4+\dfrac{1}{\sqrt[]{n}}-\dfrac{2}{n^2}\right)=-4+0-0=-4< 0\)
\(\Rightarrow\lim n^2\left(-4+\dfrac{1}{\sqrt[]{n}}-\dfrac{2}{n^2}\right)=-\infty\)

\(\Leftrightarrow4a^2+2b^2-4ab-10b+22< 0\)
\(\Leftrightarrow\left(2a-b\right)^2+\left(b-5\right)^2< 3\)
\(\Rightarrow\left(b-5\right)^2< 3\Rightarrow\left[{}\begin{matrix}\left(b-5\right)^2=0\\\left(b-5\right)^2=1\end{matrix}\right.\)
\(\Rightarrow b=\left\{4;5;6\right\}\)
- Với \(b=4\Rightarrow\left(2a-4\right)^2< 2\Rightarrow\left(a-2\right)^2< \dfrac{1}{2}\Rightarrow\left(a-2\right)^2=0\)
\(\Rightarrow a=2\)
- Với \(b=5\Rightarrow\left(2a-5\right)^2< 3\Rightarrow\left(2a-5\right)^2=1\Rightarrow\left[{}\begin{matrix}a=2\\a=3\end{matrix}\right.\) (do 2a-5 luôn lẻ)
- Với \(b=6\Rightarrow\left(2a-6\right)^2< 2\Rightarrow\left(a-3\right)^2< \dfrac{1}{2}\Rightarrow\left(a-3\right)^2=0\)
\(\Rightarrow a=3\)


Theo nguyên lý chia kẹo Euler, ta có \(C_{5-1}^{3-1}=6\) cách trao giải thưởng

ĐKXĐ: \(sin2x\ne1\Rightarrow x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{2cos2x}{1-sin2x}=0\Rightarrow cos2x=0\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Kết hợp ĐKXĐ: \(\Rightarrow x=\dfrac{3\pi}{4}+k\pi\)

4.
\(u_{n+1}=\dfrac{u_n}{3u_n+1}\Rightarrow\dfrac{1}{u_{n+1}}=\dfrac{3u_n+1}{u_n}=\dfrac{1}{u_n}+3\)
Đặt \(\dfrac{1}{u_n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{u_1}=2\\v_{n+1}=v_n+3\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số cộng với công bội \(d=3\)
\(\Rightarrow v_n=v_1+\left(n-1\right)d=2+3\left(n-1\right)=3n-1\)
\(\Rightarrow u_n=\dfrac{1}{v_n}=\dfrac{1}{3n-1}\)
6.
\(u_{n+1}=4u_n-3u_{n-1}\Leftrightarrow u_{n+1}-u_n=3\left(u_n-u_{n-1}\right)\)
Đặt \(u_{n+1}-u_n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_2-u_1=3\\v_n=3v_{n-1}\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số nhân với công bội \(q=3\)
\(\Rightarrow v_n=3.3^{n-1}=3^n\)
\(\Rightarrow u_{n+1}-u_n=3^n\)
\(\Rightarrow u_{n+1}-\dfrac{1}{2}.3^{n+1}=u_n-\dfrac{1}{2}.3^n\)
Đặt \(u_n-\dfrac{1}{2}.3^n=x_n\Rightarrow\left\{{}\begin{matrix}x_1=u_1-\dfrac{1}{2}.3^1=-\dfrac{1}{2}\\x_{n+1}=x_n\end{matrix}\right.\)
\(\Rightarrow x_{n+1}=x_n=x_{n-1}=...=x_1=-\dfrac{1}{2}\)
\(\Rightarrow u_n-\dfrac{1}{2}.3^n=-\dfrac{1}{2}\Rightarrow u_n=\dfrac{3^n-1}{2}\)

TL:
\(789302687-100=789302587\)
\(5639174929-649102=5638525827\)
_HT_
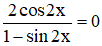
9.
Đặt \(u_n=2v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{2015}{2}\\2v_{n+1}=8v_n^3-6v_n\end{matrix}\right.\) \(\Rightarrow v_{n+1}=4v_n^3-3v_n\)
Xét số thực a là nghiệm lớn hơn của pt:
\(a^2-2v_1a+1=0\Rightarrow\left\{{}\begin{matrix}a=v_1+\sqrt{v_1^2-1}\\\dfrac{1}{a}=v_1-\sqrt{v_1^2-1}\end{matrix}\right.\)
Khi đó ta có:
\(v_1=\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\)
\(v_2=4v_1^3-3v_1=4\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]^3-3\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]\)
\(=\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)=\dfrac{1}{2}\left(a^{3^1}+\dfrac{1}{a^{3^1}}\right)\)
\(v_3=4v_2^3-3v_2=4\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]=\dfrac{1}{2}\left(a^9+\dfrac{1}{a^9}\right)=\dfrac{1}{2}\left(a^{3^2}+\dfrac{1}{a^{3^2}}\right)\)
Từ đó, ta tổng quát được: \(v_n=\dfrac{1}{2}\left(a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\right)\)
Ta chứng minh bằng quy nạp:
- Với \(n=1;2;3\) đúng như đã kiểm chứng ở trên
- Giả sử đúng với \(n=k\) hay \(v_k=\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\)
Ta cần chứng minh: \(v_{k+1}=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\)
Ta có: \(v_{k+1}=4\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]\)
\(=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)+\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)-\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\) (đpcm)
Vậy SHTQ của dãy là: \(u_n=2v_n=a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\) với \(a\) là nghiệm lớn của pt: \(x^2-2015x+1=0\)
10.
Ta có: \(u_1=1=tan\dfrac{\pi}{4}=tan\dfrac{\pi}{2^2}\)
\(u_2=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{4}}-1}{tan\dfrac{\pi}{4}}=\sqrt{2}-1=tan\dfrac{\pi}{8}=tan\dfrac{\pi}{2^3}\)
Dự đoán: \(u_n=tan\dfrac{\pi}{2^{n+1}}\)
Ta chứng minh bằng quy nạp
Với \(n=1;2\) đúng (đã kiểm chứng ở trên)
Giả sử điều đó đúng với \(n=k\) hay \(u_k=tan\dfrac{\pi}{2^{k+1}}\)
Ta cần chứng minh: \(u_{k+1}=tan\dfrac{\pi}{2^{k+2}}\)
Thật vậy, ta có:
\(u_{k+1}=\dfrac{\sqrt{1+u_k^2}-1}{u_k}=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}=\dfrac{\dfrac{1}{cos\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}\)
\(=\dfrac{1-cos\dfrac{\pi}{2^{k+1}}}{sin\dfrac{\pi}{2^{k+1}}}=\dfrac{2sin^2\dfrac{\pi}{2^{k+2}}}{2sin\dfrac{\pi}{2^{k+2}}.cos\dfrac{\pi}{2^{k+2}}}=tan\dfrac{\pi}{2^{k+2}}\) (đpcm)