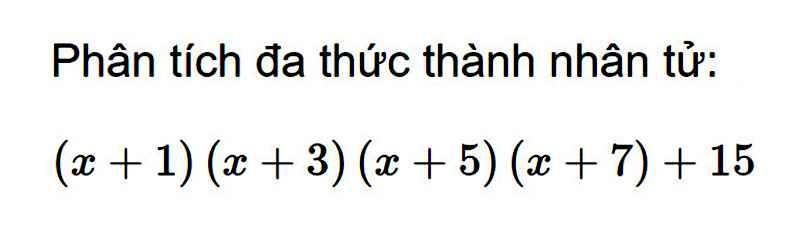Cho dãy số 0; 1; 4; 9; 16; ...; 2500. Viết tập hợp D gồm các số hạng của dãy số bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó. Tập hợp D có bao nhiêu phần tử?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H9
HT.Phong (9A5)
CTVHS
19 tháng 6
Đúng(2)
BL
3
DS
Đinh Sơn Tùng
CTVHS
VIP
19 tháng 6
Xác đinh dạng toán: Tổng dãy số
Gọi A là tổng trên
Ta có:
A = 1,1 + 1,2 +1,3 +1,4 +1,5 + 1,6 +1,7 + 1,8 + …..9,8 + 9,9
A x 10 = 11 + 12 +13 +14 +15 + 16 +17 + 18 + …..98 + 99
Số số hạng của dãy A x 10 là:
(99 - 11) : 1 + 1 = 89 (số)
=> Tổng của dãy A x 10 là:
(99 + 11) x 89 : 2 = 4895
=> Tổng dãy trên là: (A)
4895 : 10 = 489,5
Đ/S:....
~hok tốt~
@3a3sontung
19 tháng 6
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{AE}{AB}=\dfrac{CE}{CB}\)
=>\(\dfrac{AE}{6}=\dfrac{CE}{10}\)
=>\(\dfrac{AE}{3}=\dfrac{CE}{5}\)
mà AE+CE=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{3}=\dfrac{CE}{5}=\dfrac{AE+CE}{3+5}=\dfrac{8}{8}=1\)
=>\(AE=3\cdot1=3\left(cm\right)\)
b: Xét ΔBAE vuông tại A và ΔBCM vuông tại C có
\(\widehat{ABE}=\widehat{CBM}\)
Do đó: ΔBAE~ΔBCM
=>\(\widehat{BEA}=\widehat{BMC}\)
=>\(\widehat{CME}=\widehat{CEM}\)
=>ΔCEM cân tại C
NT
3
19 tháng 6
Số hạng thứ 50 sẽ là:
1+(1+2+3+...+49)
\(=1+50\cdot\dfrac{49}{2}=1+49\cdot25=1226\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 6
Giải:
Cho dãy số: 1; 2; 4; 7; 11; 16;...
Ta có: ST2 = 2 = 1 + 1
ST3 = 4 = 1 + 1+ 2
ST4 = 7 = 1 + 1+ 2+ 3
ST5 = 11 = 1 + 1+ 2+ 3+ 4
ST6 = 16 = 1 + 1+ 2 + 3 + 4 + 5
....................................................
ST50 = 1 + 1+ 2+ 3+ 4+ 5 + ... + 49
Xét dãy số: 1; 2; 3; 4; 5;...; 49 là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(49 - 1) : 1 + 1 = 49 (số hạng)
Tổng của dãy số trên là:
(49 + 1) x 49 : 2 = 1225
Vậy số thứ 50 là: 1 + 1225 = 1226
Đáp số: 1226
19 tháng 6
a: G={20;30;40}
G={\(\overline{a0}\)|\(10< \overline{a0}< 50\)}
b: H={13;22;31;40}
H={\(\overline{ab}\)|a+b=4, \(a,b\in N\), \(a\ne0\)}
VH
1
19 tháng 6
x=2024 nên x-1=2023
\(H=x^{14}-2023x^{13}-2023x^{12}-...-2023x-2023\)
\(=x^{14}-x^{13}\left(x-1\right)-x^{12}\left(x-1\right)-...-x\left(x-1\right)-\left(x-1\right)\)
\(=x^{14}-x^{14}+x^{13}-x^{13}+x^{12}-...-x^2+x-x+1\)
=1
19 tháng 6
`(x+1)(x+3)(x+5)(x+7)+15`
`=(x+1)(x+7)(x+3)(x+5)+15`
`= (x^2+7x+x+7)(x^2+5x+3x+15)+15 `
`=(x^2 +8x+7)(x^2+8x+15)+15`
Đặt `t=x^2 +8x+11`
`=(t-4)(t+4)+15`
`=t^2 -16 +15`
`=t^2 -1`
`=(t-1)(t+1)`
`=(x^2 +8x+11-1)(x^2 +8x+11+1)`
`=(x^2 +8x+10)(x^2 +8x+12)`
