Người ta trồng ngô trên một thửa ruộng hình chữ nhật chiều rộng 60 m chiều dài bằng 5353 chiều rộng. a tính diện tích thửa ruộng đó b biết rằng trung bình cứ 100m2 thu hoạch được 30 kg ngô. Hỏi trên cả thửa ruộng đó,người ta thu hoạch được bao nhiêu tạ ngô
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(2x-3\right)^9-2x+3=0\)
=>\(\left(2x-3\right)^9-\left(2x-3\right)=0\)
=>\(\left(2x-3\right)\left[\left(2x-3\right)^8-1\right]=0\)
=>\(\left[{}\begin{matrix}2x-3=0\\\left(2x-3\right)^8-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\\left(2x-3\right)^8=1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\2x-3=1\\2x-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\\x=1\end{matrix}\right.\)

a: \(101^2=\left(100+1\right)^2=100^2+2\cdot100\cdot1+1^2\)
=10000+200+1
=10201
b: \(64^2+36^2+72\cdot64\)
\(=64^2+2\cdot64\cdot36+36^2\)
\(=\left(64+36\right)^2=100^2=10000\)
c: \(54^2+46^2-2\cdot54\cdot46=\left(54-46\right)^2=8^2=64\)
d: \(98\cdot102=\left(100-2\right)\left(100+2\right)=100^2-4=9996\)

1:ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC tại H
Xét tứ giác AHCD có
O là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
2: AHCD là hình chữ nhật
=>AD//HC và AD=HC
Ta có: AD//HC
=>AD//HB
Ta có: AD=CH
mà CH=HB
nên AD=HB
Xét tứ giác ADHB có
AD//HB
AD=HB
Do đó: ADHB là hình bình hành
3: \(CH=\dfrac{CB}{2}=3\left(cm\right)\)
AHCD là hình chữ nhật
=>\(S_{AHCD}=AH\cdot HC=4\cdot3=12\left(cm^2\right)\)

1: DA=DK
=>ΔDAK cân tại D
=>\(\widehat{DAK}=\widehat{DKA}\)
mà \(\widehat{DKA}=\widehat{KAB}\)(hai góc so le trong, AB//DK)
nên \(\widehat{DAK}=\widehat{BAK}\)
=>AK là phân giác của góc BAD
2: ta có: CD=CK+KD
CD=AD+BC
Do đó: CK+KD=AD+BC
mà DA=DK
nên CK=CB
3: CK=CB
=>ΔCBK cân tại C
=>\(\widehat{CKB}=\widehat{CBK}\)
mà \(\widehat{CKB}=\widehat{ABK}\)(hai góc so le trong, AB//CK)
nên \(\widehat{ABK}=\widehat{CBK}\)
=>BK là phân giác của góc ABC

\(a.\left(x^2+5x+6\right)\left(x^2-15x+56\right)-144\\ =\left(x+2\right)\left(x+3\right)\left(x-7\right)\left(x-8\right)-144\\ =\left[\left(x+2\right)\left(x-7\right)\right]\left[\left(x+3\right)\left(x-8\right)\right]-144\\ =\left(x^2-5x-14\right)\left(x^2-5x-24\right)-144\\ =\left(x^2-5x-19+5\right)\left(x^2-5x-19-5\right)-144\\ =\left(x^2-5x-19\right)^2-5^2-144\\ =\left(x^2-5x-19\right)^2-169\\ =\left(x^2-5x+19\right)^2-13^2\\ =\left(x^2-5x-19-13\right)\left(x^2-5x-19+13\right)\\ =\left(x^2-5x-32\right)\left(x^2-5x-6\right)\\ =\left(x^2-5x-32\right)\left(x+1\right)\left(x-6\right)\)
\(b.\left(x^2-11x+28\right)\left(x^2-7x+10\right)-72\\ =\left(x-4\right)\left(x-7\right)\left(x-5\right)\left(x-2\right)-72\\ =\left[\left(x-4\right)\left(x-5\right)\right]\left[\left(x-7\right)\left(x-2\right)\right]-72\\ =\left(x^2-9x+20\right)\left(x^2-9x+14\right)-72\\ =\left(x^2-9x+17+3\right)\left(x^2-9x+17-3\right)-72\\ =\left(x^2-9x+17\right)^2-3^2-72\\ =\left(x^2-9x+17\right)^2-81\\ =\left(x^2-9x+17\right)^2-9^2\\ =\left(x^2-9x+17-9\right)\left(x^2-9x+17+9\right)\\ =\left(x^2-9x+8\right)\left(x^2-9x+26\right)\\ =\left(x-1\right)\left(x-8\right)\left(x^2-9x+26\right)\)

a: \(P=4\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^{32}-1\right)\left(3^{32}+1\right)}{2}=\dfrac{3^{64}-1}{2}\)
b: \(Q=\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\)
\(=\dfrac{\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^{16}-1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^{32}-1\right)\left(5^{32}+1\right)}{24}=\dfrac{5^{64}-1}{24}\)

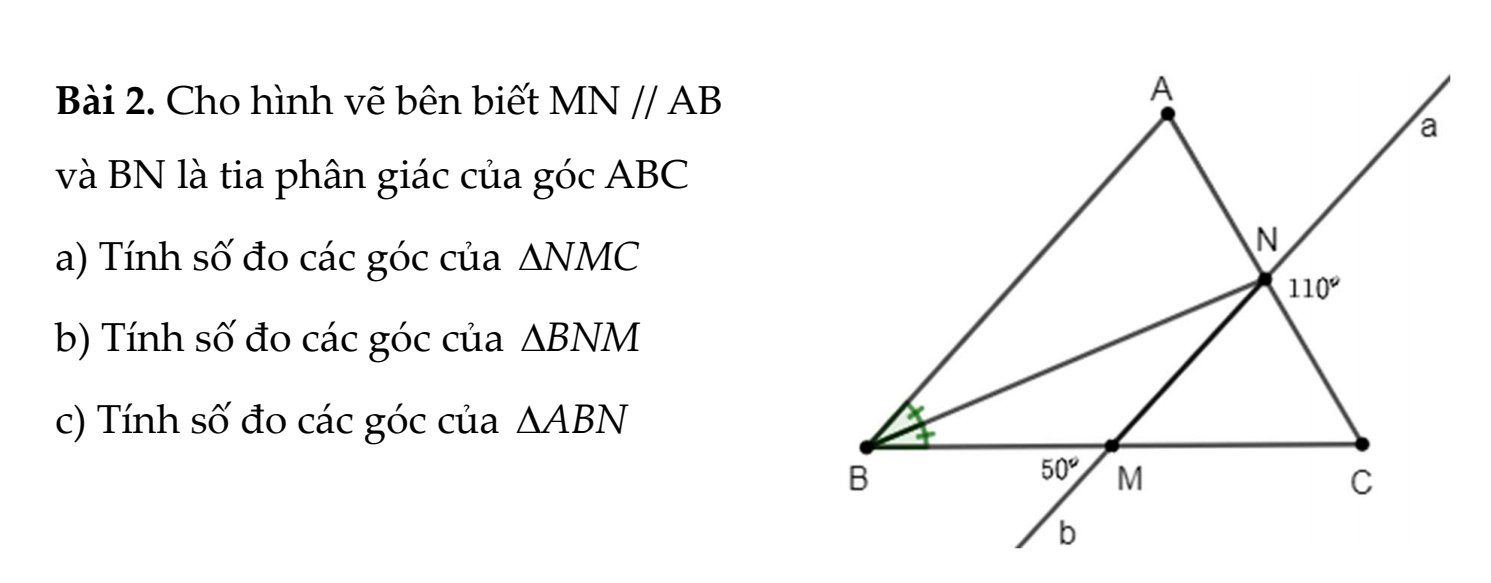
a: Ta có: \(\widehat{bMB}=\widehat{NMC}\)(hai góc đối đỉnh)
mà \(\widehat{bMB}=50^0\)
nên \(\widehat{NMC}=50^0\)
Ta có: \(\widehat{MNC}+\widehat{aNC}=180^0\)(hai góc kề bù)
=>\(\widehat{MNC}+110^0=180^0\)
=>\(\widehat{MNC}=70^0\)
Xét ΔMNC có \(\widehat{NMC}+\widehat{MNC}+\widehat{C}=180^0\)
=>\(\widehat{C}+50^0+70^0=180^0\)
=>\(\widehat{C}=60^0\)
b: Ta có: \(\widehat{NMB}+\widehat{NMC}=180^0\)(hai góc kề bù)
=>\(\widehat{NMB}+50^0=180^0\)
=>\(\widehat{NMB}=130^0\)
Ta có: MN//AB
=>\(\widehat{CMN}=\widehat{CBA}\)(hai góc đồng vị)
=>\(\widehat{CBA}=50^0\)
BN là phân giác của góc CBA
=>\(\widehat{NBM}=\dfrac{\widehat{ABC}}{2}=25^0\)
Xét ΔNMB có \(\widehat{NMB}+\widehat{BNM}+\widehat{NBM}=180^0\)
=>\(\widehat{MNB}=180^0-130^0-25^0=25^0\)
c: BN là phân giác của góc CBA
=>\(\widehat{ABN}=\dfrac{\widehat{ABC}}{2}=25^0\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAN}+60^0+50^0=180^0\)
=>\(\widehat{BAN}=70^0\)
Xét ΔBAN có \(\widehat{BAN}+\widehat{ABN}+\widehat{ANB}=180^0\)
=>\(\widehat{ANB}=180^0-75^0-25^0=85^0\)
a) Chiều dài của thửa ruộng là:
\(60\times\dfrac{5}{3}=100\left(m\right)\)
Diện tích của thửa ruộng là:
\(60\times100=6000\left(m^2\right)\)
b) Khối lượng ngô thu hoạch được là:
\(6000:100\times30=1800\left(kg\right)\)
ĐS: ...
Chiều dài thửa ruộng là:
`60` x `5 : 3 = 100 (m)`
Diện tích thửa ruộng là:
`100` x `60 = 6000 (m^2)`
`6000m^2` gấp `100m^2` số lần là:
`6000 : 100 = 60` (lần)
Số kg ngô thu được là:
`60` x `30 = 1800 (kg)`
Đổi `1800kg = 18` tạ
Đáp số: ...