có hai con đường từ A đến B và 3 con đường từ B đến C Hỏi có bao nhiêu con đường từ A đến B đến C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



$x,y$ có điều kiện gì không bạn? Như là số nguyên, số tự nhiên,....

a: \(\dfrac{3}{5}+\dfrac{3}{5\cdot9}+...+\dfrac{3}{97\cdot101}\)
\(=\dfrac{3}{4}\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{97\cdot101}\right)\)
\(=\dfrac{3}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{4}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{4}\cdot\dfrac{100}{101}=\dfrac{75}{101}\)
b: \(\dfrac{1}{18}+\dfrac{1}{54}+\dfrac{1}{108}+...+\dfrac{1}{990}\)
\(=\dfrac{1}{3\cdot6}+\dfrac{1}{6\cdot9}+...+\dfrac{1}{30\cdot33}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+...+\dfrac{3}{30\cdot33}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{3}\cdot\left(\dfrac{1}{3}-\dfrac{1}{33}\right)=\dfrac{1}{3}\cdot\dfrac{10}{33}=\dfrac{10}{99}\)
c: \(\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{99}+1\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{100}{99}=\dfrac{100}{2}=50\)
d: \(\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{2}{7}\right)\cdot...\cdot\left(1-\dfrac{2014}{7}\right)\)
\(=\left(1-\dfrac{7}{7}\right)\cdot\dfrac{6}{7}\cdot\dfrac{5}{7}\cdot...\cdot\dfrac{-2007}{7}\)
\(=\left(1-1\right)\cdot\dfrac{6}{7}\cdot\dfrac{5}{7}\cdot...\cdot\dfrac{-2007}{7}\)
=0

\(A=\dfrac{5}{40}+\dfrac{5}{88}+\dfrac{5}{154}+\dfrac{5}{238}+\dfrac{5}{340}\)
\(=\dfrac{5}{5\cdot8}+\dfrac{5}{8\cdot11}+\dfrac{5}{11\cdot14}+\dfrac{5}{14\cdot17}+\dfrac{5}{17\cdot20}\)
\(=\dfrac{5}{3}\left(\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+\dfrac{3}{11\cdot14}+\dfrac{3}{14\cdot17}+\dfrac{3}{17\cdot20}\right)\)
\(=\dfrac{5}{3}\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{17}-\dfrac{1}{20}\right)\)
\(=\dfrac{5}{3}\left(\dfrac{1}{5}-\dfrac{1}{20}\right)=\dfrac{5}{3}\cdot\dfrac{3}{20}=\dfrac{1}{4}\)

\(\dfrac{x+2}{3}=\dfrac{x-4}{5}\)
=>5(x+2)=3(x-4)
=>5x+10=3x-12
=>5x-3x=-12-10
=>2x=-22
=>\(x=-\dfrac{22}{2}=-11\)
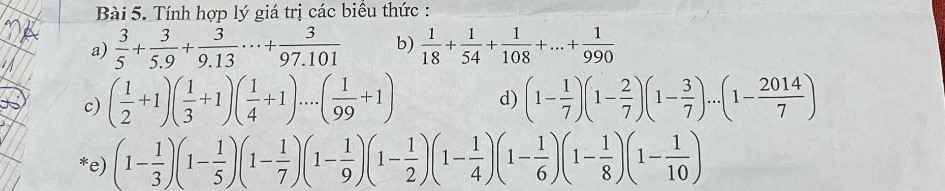
Bài giải:
Có hai cách chọn con đường đi từ A đến B
Có ba cách chọn con đường đi từ B đến C
Số con đường đi từ A đến B rồi đến C là:
2 x 3 = 6 (con đường)
Kết luận có 6 con đường đi từ A đến B rồi đến C.