Bài 1: Chứng tỏ rằng:
b)Trong ba số tự nhiên liên tiếp, luôn có một số chia hết cho 3;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cạnh của hình vuông lúc đầu cũng là chiều rộng của hình chữ nhật lúc sau là:
20:4=5 cm
Đổi : 2 m= 200 cm và 1 m = 100 cm
Chiều dài của hình chữ nhật là:
100+5+200=305 cm
Chu vi của hình chữ nhật là:
(305+5)x2=620 cm
Đáp/Số: 620 cm

47 x 8 - 27 x 9 + 47 x 12 - 27 x 11
= 47 x ( 8 + 12 ) - 27 x ( 9 - 11 )
= 47 x 20 - 27 x ( - 2 )
= 940 + 54
= 994


Nếu mua ở cửa hàng A thì bạn Tú sẽ phải trả số tiền là:
(810 000 + 1 290 000):2 = 2 100 000:2 = 1 050 000(đồng).
Nếu mua ở cửa hàng B thì bạn Tú sẽ mua đôi 1 290 000 đồng và được tặng đôi 810 000 đồng. Do đó số tiền phải trả là: 1 290 000 đồng.
Vậy bạn Tú nên mua giày ở cửa hàng A thì có giá rẻ hơn.

Số máu các cán bộ công nhân viên trên địa bàn thành phố Hà Nội đã hiến được là:
1 000.450 = 450 000 (ml)
Ta có: 450 000:1 500 = 300 nên với số máu được hiến tặng này sẽ cấp cứu được cho 300 bệnh nhân.

Một giá sách có thể xếp được số quyển sách là: 11.32 = 352 (quyển sách).
Ta có: 5 628:352 = 15 (dư 348) nên xếp đủ vào 15 giá sách thì còn thừa 348 quyển sách chưa được xếp. Do đó phải dùng thêm một giá sách nữa để xếp 348 quyển sách trên.
Vậy cần ít nhất: 15 + 1 = 16 (giá sách).

a)
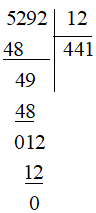
Vậy 5 292:12 = 441.
b)
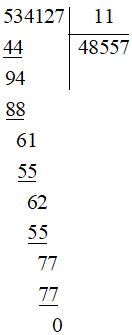
Vậy 534 127:11 = 48 557.
c)
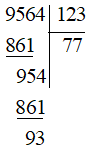
Vậy 9 564:123 = 77 (dư 93).
d)
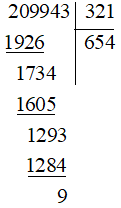
Vậy 209 943:321 = 654 (dư 9).

Số ngày trong một tuần lễ là 7 ngày thì gấp đôi số ngày trong một tuần lễ là 14.
Suy ra = 14.
Gấp đôi là 14.2 = 28.
Vì gấp đôi của nên = 28.
Vậy năm đó là năm 1428.
Bạn ht

\(4-2n\)\(=2n+2-6\)
\(2\left(n+1\right)\)\(-6\)
\(2\left(n+1\right)\)Chia hết cho \(1+n\)
=>6 chia hết cho 1+n
Ư(6)={1,-1,2,-2,3,-3,6,-6}
| \(1+n\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) | \(6\) | \(-6\) |
| \(n\) | \(0\) | \(-2\) | \(1\) | \(-3\) | \(2\) | \(-4\) | \(5\) | \(-7\) |
=>.............




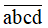
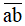 gấp đôi số ngày trong một tuần lễ, còn
gấp đôi số ngày trong một tuần lễ, còn 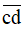 gấp đôi của
gấp đôi của 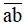 . Tính xem năm đó là năm nào.
. Tính xem năm đó là năm nào.
a) Gọi 3 số tự nhiên liên tiếp là x,x+1,x+2(x∈N)x,x+1,x+2(x∈N)
- Nếu x=3kx=3k ( thỏa mãn ). Nếu x=3k+1x=3k+1 thì x+2=3k+1+2=(3k+3)⋮3x+2=3k+1+2=(3k+3)⋮3
- Nếu x=3k+2x=3k+2 thì x+1=3k+1+2=(3k+3)⋮3x+1=3k+1+2=(3k+3)⋮3
Vậy trong 3 số tự nhiên liên tiêp có 1 số chia hết cho 3.
b) Nhận thấy 17n,17n+1,17n+217n,17n+1,17n+2 là 3 số tự nhiên liên tiếp mà 17n17n không chia hết cho 3, nên trong 2 số còn lại 1 số phải ⋮3⋮3
Do vậy: A=(17n+1)(17n+2)⋮3A=(17n+1)(17n+2)⋮3
Đặt 3 số tự nhiên liên tiếp là: n, n+1, n+2
Giả sử n⋮ 3 thì thỏa mãn đề bài
Giả sử n chia 3 dư 1 thì n=3k+1 ⇒ n+2=3k+3⋮ 3 ⇒ thỏa mãn đề bài
Giả sử n chia 3 dư 2 thì n=3k+2 ⇒ n+1=3k+3⋮ 3 ⇒ thỏa mãn đề bài
Vậy trong 3 số tự nhiên liên tiếp thì luô có 1 số chi hết cho 3
HT Ạ ( NGUỒN GG)