góc xOy là góc tù. Từ điểm O vẽ 12 tia nằm tạo thành góc xOy. trong hình có bao nhiêu góc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\dfrac{x}{3}\) = \(\dfrac{y}{5}\) = \(\dfrac{2x-y}{3.2-5}\) = \(\dfrac{11}{1}\)
=> x = 11 . 3 = 33; y = 11 . 5 = 55

Bài làm
Người lính trong bài đồng dao mùa xuân là những người anh hùng, những người đã hy sinh vì đất nước, vì dân tộc. Em cảm thấy rất ngưỡng mộ và tự hào về những người lính, về tinh thần yêu nước, quyết tâm đánh đuổi giặc ngoại xâm của họ. Em cũng cảm nhận được sự gắn bó với thiên nhiên, với mùa xuân của những người lính. Họ không chỉ chiến đấu mà còn biết hát, biết thơ, biết yêu đời. Sự ngây thơ của một đứa trẻ bị che đi bởi sự mạnh mẽ, can trường của một người lính đã khiến em càng thêm yêu mến và kính trọng họ. Chính các người lính đã làm nên mùa xuân của đất nước, tương lai của nhân dân. Đó chính là những người vĩ đại nhất, cao cả nhất mà muôn đời dân tộc ta vẫn biết ơn và cảm phục.

x - 2 = 1/3 x + 1/3
x - 1/3 x = 1/3 + 2
2/3 x = 7/3
x = 7/3 : 2/3
x = 7/2

\(155-10\left(x+1\right)=55\\ \Rightarrow10\left(x+1\right)=155-55\\ \Rightarrow10\left(x+1\right)=100\\ \Rightarrow x+1=100:10\\ \Rightarrow x+1=10\\ \Rightarrow x=10-1\\ \Rightarrow x=9\)
`155-10(x+1)=55`
`10(x+1)=155-55`
`10(x+1)=100`
`x+1=100:10`
`x+1=10`
`x=10-1`
`x=9`

\(4^n\times2^3=384\\ \Leftrightarrow4^n=384:2^3\\ \Leftrightarrow4^n=48\)
Bạn kiểm tra lại đề nha.

\(M=\left(100-1\right)\left(100-2^2\right)...\left(100-50^2\right)\)
\(M=\left(100-1\right)\left(100-2^2\right)...\left(100-10^2\right)...\left(100-50^2\right)\)
\(M=\left(100-1\right)\left(100-2^2\right)...\left(100-100\right)...\left(100-50^2\right)\)
\(M=\left(100-1\right)\left(100-2^2\right)...0...\left(100-50^2\right)\)
\(M=0\)

\(\left(0,0625\right)^2=\left(0,5^4\right)^2\)
\(=0,5^{4\cdot2}\)
\(=0,5^8\)
\(\left(0,0625\right)^2=\left[\left(0,5\right)^4\right]^2=\left(0,5\right)^8\)

Ta đặt:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(a=b\times k\) ; \(c=d\times k\)
a) Ta có: \(\dfrac{a}{b}=\dfrac{b\times k}{d\times k}=\dfrac{b}{d}\) (1)
=> \(\dfrac{a+b}{c+d}=\dfrac{b\times k+b}{d\times k+d}=\dfrac{b\times\left(k+1\right)}{d\times\left(k+1\right)}=\dfrac{b}{d}\) (2)
Từ (1),(2) => đpcm
b)
\(\dfrac{a+b}{a}=\dfrac{b\times k+b}{b\times k}=\dfrac{b\times\left(k+1\right)}{b\times k}=\dfrac{k+1}{k}\) (1)
\(\dfrac{c+d}{c}=\dfrac{d\times k+d}{d\times k}=\dfrac{d\times\left(k+1\right)}{d\times k}=\dfrac{k+1}{k}\) (2)
Từ (1),(2) => đpcm
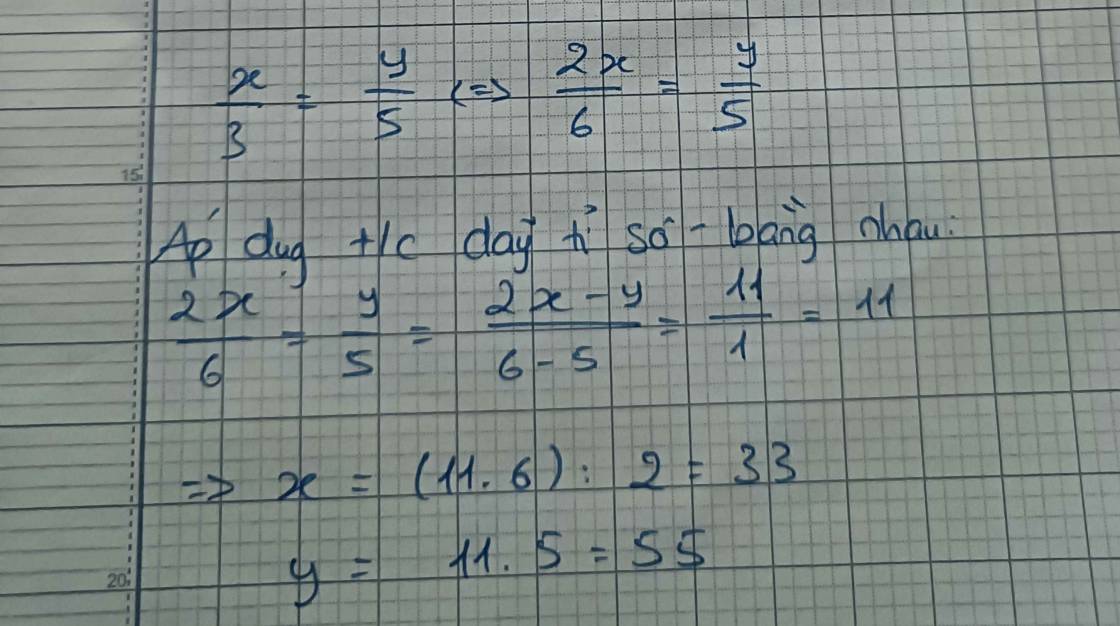
Số góc 12 tia chung gốc tạo thành là:
\(\dfrac{n.\left(n-1\right)}{2}=\dfrac{12.\left(12-1\right)}{2}=66\) ( góc )
Vậy có 66 góc được tạo bởi 12 tia chung gốc.