Nếu đoàn xe vận tải có 15 xe tải lớn và 4 xe tải nhỏ tất cả chở 178 tấn hàng. Biết mỗi xe tải lớn chở nhiều hơn xe tải nhỏ là 3 tấn. Tính số tấn hàng mỗi xe tải từng loại đã trở?( các bạn giúp mình với nhé Mình cần gấp)😙😙
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 1 2018
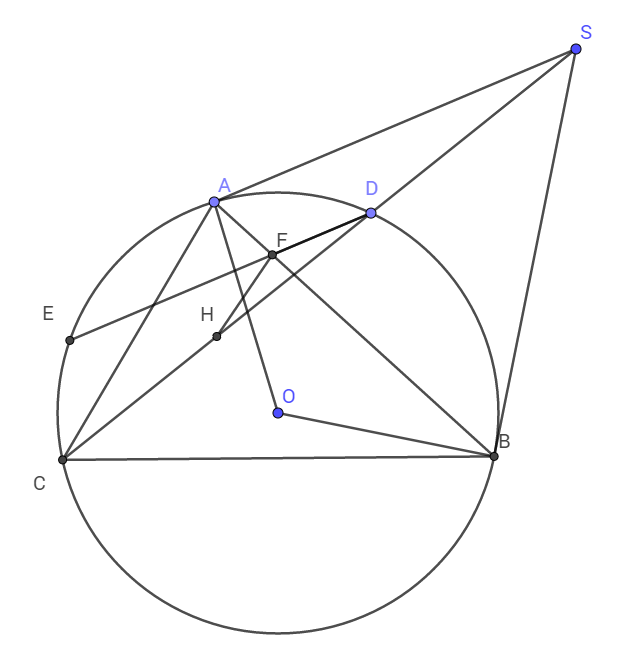
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
S
0
S
0
DM
Doãn Minh Cường
Giáo viên
31 tháng 1 2018
Áp dụng bất đẳng thức Cô si cho ba số dương ta có \(a+b+c\ge3\sqrt[3]{abc}\) và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{3}{\sqrt[3]{abc}}\). Do đó nếu đặt \(t=\sqrt[3]{abc}\) t hì \(a+b+c+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\left(t+\frac{1}{t}\right)\) . Chú ý rằng từ giả thiết
\(\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=1\) suy ra \(a^2+b^2+c^2=abc\) từ đó
\(abc=a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow a^3b^3c^3\ge27a^2b^2c^2\Rightarrow abc\ge27\)\(\Rightarrow t\ge3\).
Do đó \(t+\frac{1}{t}=\frac{8t}{9}+\frac{t}{9}+\frac{1}{t}\ge\frac{8.3}{9}+2\sqrt{\frac{t}{9}.\frac{1}{t}}=\frac{10}{3}\). Suy ra
\(a+b+c+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\left(t+\frac{1}{t}\right)\ge\frac{3.10}{3}=10\)
Đẳng thức xảy ra khi và chỉ khi \(\hept{\begin{cases}a=b=c>0\\t=\sqrt[3]{abc}=3\\a^2+b^2+c^2=abc\end{cases}}\)\(\Leftrightarrow a=b=c=3\).
KV
0
Giả sử 4 xe tải nhỏ mỗi xe tăng thêm 3 tấn, tức là tương đương có thêm 12 kg và thêm 4 xe tải lớn. Khi đó, tổng số tấn hàng là 178 + 12 = 190 tấn, tương ứng với 15 +4 = 19 xe tải lớn. Vậy, mỗi xe tải lớn chở 190 : 19 = 10 (tấn) và xe tải nhỏ chở 10 - 3 = 7 ( tấn).
Check: 15 * 10 + 4 * 7 = 178 (tấn)
Thêm 12 tấn hàng bạn nhé. Quen tay đánh nhầm thành kg :D