a. A = |x + 2| + 3

Để A đạt gá trị nhỏ nhất thì |x + 2| + 3 đạt giá trị nhỏ nhất

=> |x + 2| = 0

=> x + 2 = 0

=> x = -2

Thay vào, ta có:

A = |-2 + 2| + 3 = 0 + 3 = 3

Vậy A đạt giá nhỏ nhất <=> x =-2

b. B = |2 - 3| - 1 = 1 - 1 = 0      (?)

c. C = |x + 1| + |2 - x|

Vì |x + 1| \(\ge\) 0, |2 - x| \(\ge\) 0

Để C đạt giá trị nhỏ nhất thì |x + 1| + |2 - x| = 0

=> \(\hept{\begin{cases}\left|x+1\right|=0\\\left|2-x\right|=0\end{cases}}\) => \(\hept{\begin{cases}x+1=0\\2-x=0\end{cases}}\) => \(\hept{\begin{cases}x_1=-1\\x_2=2\end{cases}}\)

Thay vào, ta có:

|x + 1| + |2 - x| = |-1 + 1| + |2 - 2| = 0 + 0 = 0

Vậy C đạt giá trị nhỏ nhất <=> \(x_1=-1;x_2=2\)

d. D = |3x + 1| + |3x - 2|

Vì |3x + 1| \(\ge\) 0, |3x - 2| \(\ge\) 0

Để D đạt giá trị nhỏ nhất thì |3x + 1| + |3x - 2| = 0

=> \(\hept{\begin{cases}\left|3x+1\right|=0\\\left|3x-2\right|=0\end{cases}}\) => \(\hept{\begin{cases}3x+1=0\\3x-2=0\end{cases}}\) => \(\hept{\begin{cases}3x=-1\\3x=2\end{cases}}\) => \(\hept{\begin{cases}x_1=\frac{-1}{3}\\x_2=\frac{2}{3}\end{cases}}\)

Thay vào, ta có:

\(\left|3\cdot\frac{-1}{3}+1\right|+\left|3\cdot\frac{2}{3}-2\right|=0+0=0\)

Vậy D đạt giá trị nhỏ nhất <=> \(x_1=\frac{-1}{3};x_2=\frac{2}{3}\)

Ta có: 2^x + 2^y = 2^{x + y}

=> 2^x + 2^y - 2^{x + y} = 0

=> 2^x + 2^y - 2^x . 2^y = 0

=> 2^x . (1 - 2^y) + 2^y = 0

=> 2^x . (1 - 2^y) - (1 - 2^y) =  -1

=> (1 - 2^y)(2^x - 1) = -1

Lập bảng:

 Vậy x = y = 1

Tổng mức sản xuất của người 1 và 2 :

     5 + 3 = 8 ( phần )

Người thứ 3 bằng 25% tổng trên

=> Mức sản xuất người thứ 3 :

         25 . 8 : 100 = 2 ( phần )

Tổng mức sản xuất của 3 người :

     5 + 3 + 2 = 10 ( phần )

Số tiền người 1 được thưởng :

     10 000 000 . 5 : 10 = 5 000 000 ( đồng )

Số tiền người 2 được thưởng :

     10 000 000 . 3 : 10 = 3 000 000 ( đồng )

Số tiền người 3 được thưởng :

     10 000 000 . 2 : 10 = 2 000 000

Đề bài sai bạn ơi!

\(10.3^x=81\)

\(3^x=80:10\)

\(3^x=8\)

\(\Rightarrow3^x=\varnothing\)

\(20-\left(x-1\right)^3=\frac{1}{16}\)

\(\left(x-1\right)^3=20-\frac{1}{16}\)

\(\left(x-1\right)^3=\frac{320}{16}-\frac{1}{16}\)

\(\left(x-1\right)^3=\frac{319}{16}\)

\(\Rightarrow\left(x-1\right)^3=\varnothing\Leftrightarrow x=\varnothing\)

\(2-\left(\frac{-3}{2}\right)^0+\frac{16}{4}:\frac{1}{2}\)

\(=2-1+4:\frac{1}{2}\)

\(=1+8=9\)

2-\(\left(\frac{-3}{2}\right)^0\)+\(\frac{16}{4}\):\(\frac{1}{2}\)

=2-1+\(\frac{4}{1}\):\(\frac{1}{2}\)

=1+\(\frac{4}{1}\)x \(\frac{2}{1}\)

=1+\(\frac{4\cdot2}{1\cdot1}\)

=1+\(\frac{8}{1}\)

=1+8=9

\(\sqrt{\frac{25}{81}}-1\frac{5}{9}+\left(-1\right)^{2015}+4\sqrt{\frac{1}{4}}\)

\(=\frac{5}{9}-1-\frac{5}{9}-1+4.\frac{1}{2}\)

\(=-2+2=0\)

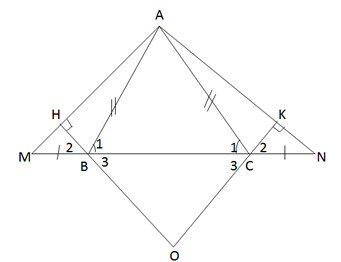
a) ∆ABC cân, suy ra  ˆB1=ˆC1B1^=C1^

 ⇒ˆABM=ˆACN⇒ABM^=ACN^

∆ABM và ∆CAN có:

AB = AC (gt)

ˆABM=ˆACNABM^=ACN^ 

BM = ON (gt)

Suy ra ˆM=ˆNM^=N^

=>∆AMN là tam giác cân ở A.

b) Hai tam giác vuông ∆BHM và ∆CKN có :

BM = CN (gt)

ˆM=ˆNM^=N^ (CM từ câu a)

Nên ∆BHM  = ∆CHN (cạnh huyền, góc nhọn)

Suy ra BH = CK.

c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)

Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).

Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK

Vậy AH = AK.

d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^  

Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)

Nên ˆB3=ˆC3B3^=C3^ .

Vậy ∆OBC là tam giác cân.

e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.

+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.

Do đó: AB = BC = AC = BM = CN

ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 60⁰)

∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .

Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .

Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200

Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.

+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)

Suy ra ˆB3=600B3^=600

Tương tự ˆC3=600C3^=600

Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.

(Tam giác cân có một góc bằng 60⁰ nên là tam giác đều).

b)

(x-7)^x+1 - (x-7)^x+11  = 0

=>(x-7)^x+1.[1-(x-7)¹⁰]=0

=>(x-7)^x+1=0 hoặc 1-(x-7)¹⁰=0

=>x-7=0 hoặc (x-7)¹⁰=1

=>x=7 hoặc x-7=1 hoặc x-7=-1

=>x=7 hoặc x=8 hoặc x=6

a)

(x-1)^x+2=(x-1)^x+6

(x-1)^x+2-(x-1)^x+6=0

(x-1)^x+2 . [1-(x-1)⁴]=0

=> (x-1)^x+2=0 hoặc 1-(x-1)⁴=0

=>x-1=0                =>(x-1)⁴=1

=>x=1                   =>x-1=1 hoặc x-1=-1

                             => x=2 hoặc x=0

vậy x \(\in\) {0;1;2}