Cách 1 :\(10:5+5:5=2+1=3\)

Cách 2 : \(10:5+5:5=\dfrac{10}{5}+\dfrac{5}{5}=\dfrac{5}{5}.\left(2+1\right)=1.3=3\)

Cách 1 :

10 : 5 + 5 : 5 

= 2+1

= 3

Cách 2 :

10 : 5 + 5 : 5

= 10/5 + 5/5 

= 10+5/5

= 15/5 

= 3

vì thích 

một ngón tay vs một ngón tay thì là bn:))

a/ 

\(MP\perp AC;NA\perp AC\) => MP//NA

\(MN\perp AB;PA\perp AB\) => MN//PA

=> ANMP là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

Ta có \(\widehat{A}=90^o\)

=> ANMP là hình chữ nhật (hbh có 1 góc vuông là HCN)

b/

MN//PA (cmt) => MN//AC

MB=MC (gt)

=> NA=NB (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

C/m tương tự cũng có PA=PC

Ta có

MP//NA (cmt) => MP//NB

NA=NB; PA=PC => NP là đường trung bình của tg ABC

=> NP//BC => NP//MB

=> BMPN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

c/

Xét HCN ANMP có

FM=FA (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)

EM=EB (gt)

=> EF là đường trung bình của tg MAB => EF//AB

=> ABEF là hình thang

Ta có

MB=MC => AM=MB=MC=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

Ta có

FM=FA=AM/2

EB=EM=BM/2

=> FA=EB

=> ABEF là hình thang cân

d/

\(\dfrac{240.50+48.100}{42.37+21.126}\)

\(=\dfrac{24.5.10.10+48.100}{42.37+3.7.6.21}\)

\(=\dfrac{100.100+48.100}{42.37+42.63}\)

\(=\dfrac{100.\left(100+48\right)}{42.\left(37+63\right)}\)

\(=\dfrac{100.148}{42.100}\)

\(=\dfrac{148}{42}\)

\(=\dfrac{74}{21}\)

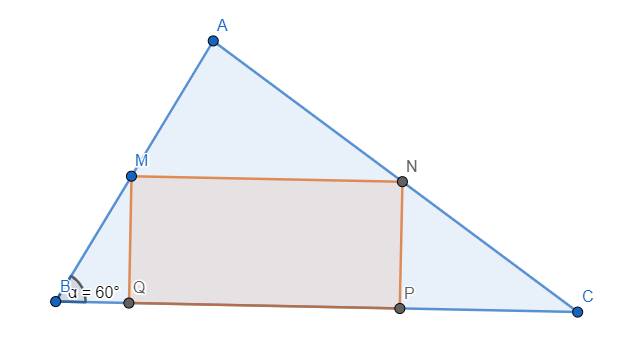
 Đặt \(MB=m>0\). \(\Rightarrow MQ=NP=\dfrac{m}{\sqrt{3}}\)

 Đặt \(AB=b>m\). Khi đó \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\) 

\(\Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{\left(b-m\right).a}{b}=\left(1-\dfrac{m}{b}\right).a\) \(=a-\dfrac{a}{b}.m\)

\(\Rightarrow S_{MNPQ}=MN.NP=\dfrac{1}{\sqrt{3}}m\left(a-\dfrac{a}{b}.m\right)\)

\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+bm\right)\)

 \(=\dfrac{a}{b\sqrt{3}}\left(-m^2+2m.\dfrac{b}{2}-\dfrac{b^2}{4}+\dfrac{b^2}{4}\right)\) 

\(=\dfrac{a}{b\sqrt{3}}\left[-\left(m-\dfrac{b}{2}\right)^2+\dfrac{b^2}{4}\right]\)

\(=-\dfrac{a}{\sqrt{3}}\left(m-\dfrac{b}{2}\right)^2+\dfrac{ab}{4\sqrt{3}}\) \(\le\dfrac{ab}{4\sqrt{3}}\), suy ra \(S_{MNPQ}\le\dfrac{ab}{4\sqrt{3}}\)

 Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{b}{2}\) hay M là trung điểm của đoạn AB.

 Vậy để diện tích hình chữ nhật MNPQ lớn nhất khi và chỉ khi M là trung điểm AB.

tổng 3 số đã cho là: 75 x 3 = 225

số thứ nhất gấp 10 lần số thứ hai, số thứ ba gấp 4 lần số thứ hai.

do đó số thứ hai là: 225 :(10+4+1)= 15

số thứ nhất là: 15 x 10= 150

số thứ ba là: 15 x 4= 60

giúp em với

Gọi x là số lượng sách tham khảo của trường trung học cơ sở A.

Theo đề bài, ta có:

(x-5): 12

(x-5): 15

(x-5): 18

250

\(A=\dfrac{3}{7x10}+\dfrac{3}{10x13}+\dfrac{3}{13x16}+...+\dfrac{3}{97x100}\)

\(A=3x\left(\dfrac{1}{7x10}+\dfrac{1}{10x13}+\dfrac{1}{13x16}+...+\dfrac{1}{97x100}\right)\)

\(A=3x\dfrac{1}{3}x\left(\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)

\(A=3x\dfrac{1}{3}x\left(\dfrac{1}{7}-\dfrac{1}{100}\right)\)

\(A=1x\left(\dfrac{100}{700}-\dfrac{7}{700}\right)=\dfrac{93}{700}\)