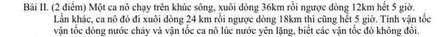
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều rộng của miếng đất là \(x\left(đv:m;x>0\right)\)
Chiều dài gấp 3 lần chiều rộng nên chiều dài miếng đất là \(3x\left(m\right)\)
Chu vi hình chữ nhật bằng 80m nên ta có pt \(2\left(x+3x\right)=80\Leftrightarrow4x=40\Leftrightarrow x=10\)(nhận)
Vậy chiều rộng của mảnh vườn là 10m và chiều dài mảnh vườn là \(3.10=30\left(m\right)\)


\(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
\(=\sqrt{\frac{8+2\sqrt{7}}{2}}-\sqrt{\frac{8-2\sqrt{7}}{2}}\)
\(=\sqrt{\frac{7+2\sqrt{7}+1}{2}}-\sqrt{\frac{7-2\sqrt{7}+1}{2}}\)
\(=\sqrt{\frac{\left(\sqrt{7}+1\right)^2}{2}}-\sqrt{\frac{\left(\sqrt{7-1}\right)^2}{2}}\)
\(=\frac{|\sqrt{7}+1|}{\sqrt{2}}-\frac{|\sqrt{7}-1|}{\sqrt{2}}\)
\(=\frac{\sqrt{7}+1-\sqrt{7}+1}{\sqrt{2}}\)
\(=\frac{2}{\sqrt{2}}=\sqrt{2}\)
bằng 100000000000000000000000000000000000000000000000000000000000000000000000000000000000tỷ

\(\hept{\begin{cases}\frac{14}{x-y+2}-\frac{10}{x+y-1}=9\\\frac{3}{x-y+2}+\frac{2}{x+y-1}=4\end{cases}}\)
Đặt x-y=a;x+y=b
\(\hept{\begin{cases}\frac{14}{a+2}-\frac{10}{b-1}=9\\\frac{3}{a+2}+\frac{2}{b-1}=4\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{14}{a+2}-\frac{10}{b-1}=9\\\frac{15}{a+2}+\frac{10}{b-1}=20\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{29}{a+2}=29\\\frac{3}{a+2}+\frac{2}{b-1}=4\end{cases}\Leftrightarrow\hept{\begin{cases}a=-1\\\frac{2}{b-1}=7\end{cases}\Leftrightarrow}\hept{\begin{cases}a=-1\\b=\frac{9}{7}\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x-y=-1\\x+y=\frac{9}{7}\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{7}\\y=\frac{8}{7}\end{cases}}}\)
Vậy....

\(\hept{\begin{cases}2x-5y=11\\3x+4x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3.\left(2x-5y\right)=3.11\\2.\left(3x+4y\right)=2.5\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6x-15y=33\\6x+8y=10\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6x-15y-\left(6x+8y\right)=33-10\\3x+4y=5\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}-23y=23\\3x+4y=5\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}y=-1\\3x-4=5\end{cases}\Leftrightarrow\hept{\begin{cases}y=-1\\x=3\end{cases}}}\)
Vậy....
Có 2 phương pháp giải hệ phương trình:
1.Phương pháp thế
2.Phương pháp cộng đại số
Ở Hệ phương trình này làm theo phương pháp thế nó khá là phức tạp nên ta dùng phương pháp cộng đại số.
Gọi vận tốc của ca nô khi nước lặng và vận tốc dòng nước lần lượt là \(x;y\left(x>y>0\right)\)
Khi đó vận tốc của ca nô lúc xuôi dòng là \(x+y\left(km/h\right)\)và vận tốc của ca nô lúc ngược dòng là \(x-y\left(km/h\right)\)
Lần thứ nhất, thời gian ca nô đi xuôi dòng là \(\frac{36}{x+y}\left(h\right)\)và thời gian ca nô đi ngược dòng là \(\frac{12}{x-y}\left(h\right)\)
Vì tổng thời gian ca nô đi xuôi và ngược dòng trong lần đi thứ nhất là 5 giờ nên ta có pt \(\frac{36}{x+y}+\frac{12}{x-y}=5\)(1)
Lần thứ hai, thời gian ca nô đi xuôi dòng là \(\frac{24}{x+y}\left(h\right)\)và thời gian ca nô đi ngược dòng là \(\frac{18}{x-y}\left(h\right)\)
Vì tổng thời gian ca nô đi xuôi và ngược dòng trong lần đi thứ hai cũng là 5 giờ nên ta có pt \(\frac{24}{x+y}+\frac{18}{x-y}=5\)(2)
Từ (1) và (2), ta có hpt \(\hept{\begin{cases}\frac{36}{x+y}+\frac{12}{x-y}=5\\\frac{24}{x+y}+\frac{18}{x-y}=5\end{cases}}\)(*)
Đặt \(\hept{\begin{cases}\frac{12}{x+y}=a\\\frac{6}{x-y}=b\end{cases}}\), khi đó (*) trở thành \(\hept{\begin{cases}3a+2b=5\\2a+3b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}9a+6b=15\\4a+6b=10\end{cases}}\Leftrightarrow\hept{\begin{cases}5a=5\\3a+2b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\left(nhận\right)\\3.1+2b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}\left(nhận\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{12}{x+y}=1\\\frac{6}{x-y}=1\end{cases}}\Rightarrow\hept{\begin{cases}x+y=12\\x-y=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=9\\y=3\end{cases}\left(nhận\right)}\)
Vậy vận tốc của ca nô lúc nước lặng là 9km/h và vận tốc dòng nước là 3km/h
P/s: Ca nô đi hơi chậm nha, không biết mình có tính sai chỗ nào không nữa.