
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1B:
a)
\(\dfrac{-1}{16}+\dfrac{-1}{24}\\ =\dfrac{-3}{48}+\dfrac{-2}{48}\\ =\dfrac{-5}{48}\)
b)
\(\dfrac{-1}{8}-\dfrac{3}{20}\\ =\dfrac{-5}{40}-\dfrac{6}{40}\\ =\dfrac{-11}{40}\)
c)
\(-\dfrac{18}{10}+0,4\\ =\dfrac{-9}{5}+\dfrac{2}{5}\\ =\dfrac{-7}{5}\)
d)
\(6,5-\left(-\dfrac{1}{5}\right)\\ =\dfrac{13}{2}+\dfrac{1}{5}\\ =\dfrac{65}{10}+\dfrac{2}{10}\\ =\dfrac{67}{10}\)

\(A=\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\\ 2A=1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\\ 2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\right)\\ A=1+\left(\dfrac{2}{2}-\dfrac{1}{2}\right)+\left(\dfrac{3}{2^2}-\dfrac{2}{2^2}\right)+...+\left(\dfrac{2023}{2^{2022}}-\dfrac{2022}{2^{2022}}\right)+\dfrac{2023}{2^{2023}}\\ A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}+\dfrac{2023}{2^{2023}}\\ 2A=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\\ 2A-A=\left(3+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}\right)\\ A=\left(3-1\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{2^2}-\dfrac{1}{2^2}\right)+...+\left(\dfrac{1}{2^{2021}}-\dfrac{1}{2^{2021}}\right)-\dfrac{2023}{2^{2023}}-\dfrac{1}{2^{2022}}\\ A=2-\dfrac{2023+2}{2^{2023}}\\ A=2-\dfrac{2025}{2^{2023}}< 2\\ \)
@ Phong Lần sau em nên chú ý về dấu như vậy bài làm sẽ hoàn hảo em nhé!

Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Tổng của ba số là 264 nên a+a+1+a+2=264
=>3a=261
=>a=261:3=87
Vậy: Ba số tự nhiên liên tiếp cần tìm là 87;87+1=88;87+2=89

Gọi ba số tự nhiên chẵn liên tiếp là a;a+2;a+4
Tổng của số lớn nhất và số bé nhất là 644 nên a+a+4=644
=>2a=640
=>a=320
Vậy: ba số cần tìm là 320;320+2=322;320+4=324

Tổng số tuổi của hai mẹ con hiện tại là:
34+5+5=44(tuổi)
Tổng số phần bằng nhau là 2+9=11(phần)
Tuổi con là 44:11x2=8(tuổi)
Tuổi mẹ là 44-8=36(tuổi)
Giải:
Tuổi của mẹ và tuổi con hiện nay là:
34 + 5 x 2 = 44 (tuổi)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Tuổi mẹ hiện nay là:
44 : (2 + 9) x 9 = 36 (tuổi)
Tuổi con hiện nay là:
44 - 36 = 8 (tuổi)
Đáp số: Tuổi con hiện nay là 8 tuổi
Tuổi mẹ hiện nay là 36 tuổi

a: ta có: \(\widehat{KAC}+\widehat{KAB}=\widehat{BAC}=90^0\)
\(\widehat{KAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
Do đó: \(\widehat{KAC}=\widehat{HBA}\)
Xét ΔKAC vuông tại K và ΔHBA vuông tại H có
AC=BA
\(\widehat{KAC}=\widehat{HBA}\)
Do đó: ΔKAC=ΔHBA
=>AK=BH
b: Ta có: ΔABC vuông cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Ta có: \(\widehat{HAM}+\widehat{HEM}=90^0\)(ΔEMA vuông tại E)
\(\widehat{HBM}+\widehat{AEB}=90^0\)(ΔEHB vuông tại H)
=>\(\widehat{HBM}=\widehat{HAM}=\widehat{KAM}\)
c: Xét ΔEHB vuông tại H và ΔEMA vuông tại M có
\(\widehat{HEB}\) chung
Do đó: ΔEHB~ΔEMA
=>\(\dfrac{EH}{EM}=\dfrac{EB}{EA}\)
=>\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
Xét ΔEHM và ΔEBA có
\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
\(\widehat{HEM}\) chung
Do đó: ΔEHM~ΔEBA
=>\(\widehat{EHM}=\widehat{EBA}=45^0\)
Xét tứ giác AMKC có \(\widehat{AMC}=\widehat{AKC}=90^0\)
nên AMKC là tứ giác nội tiếp
=>\(\widehat{AKM}=\widehat{ACM}=45^0\)
Xét ΔMHK có \(\widehat{MHK}+\widehat{MKH}=45^0+45^0=90^0\)
nên ΔMHK vuông cân tại M

Câu 8b:
\(4\dfrac{209}{245}:\left(\dfrac{3}{5}+\dfrac{4}{7}\right)+4\dfrac{209}{245}:\left(\dfrac{2}{5}+\dfrac{3}{7}\right)\)
\(=4\dfrac{209}{245}:\dfrac{41}{35}+4\dfrac{209}{245}:\dfrac{29}{35}\)
\(=4\dfrac{209}{245}\cdot\dfrac{35}{41}+4\dfrac{209}{245}\cdot\dfrac{35}{29}\)
\(=\left(4+\dfrac{209}{245}\right)\left(\dfrac{35}{41}+\dfrac{35}{29}\right)\)
\(=\dfrac{1189}{245}\cdot35\left(\dfrac{1}{41}+\dfrac{1}{29}\right)\)
\(=\dfrac{1189}{7}\cdot\dfrac{70}{1189}=\dfrac{70}{7}=10\)

a:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
Sửa đề: \(A=\sqrt{x}:\left(\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}+\dfrac{x+2}{x\sqrt{x}-1}\right)\)
\(=\sqrt{x}:\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-x-\sqrt{x}-1+x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x-1-\sqrt{x}+1}=\dfrac{\left(x-\sqrt{x}\right)\left(x+\sqrt{x}+1\right)}{x-\sqrt{x}}\)
\(=x+\sqrt{x}+1\)
b: Để A=7 thì \(x+\sqrt{x}+1=7\)
=>\(x+\sqrt{x}-6=0\)
=>\(\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)=0\)
=>\(\sqrt{x}-2=0\)(Vì \(\sqrt{x}+3>0\forall x\) thỏa mãn ĐKXĐ)
=>x=4(nhận)

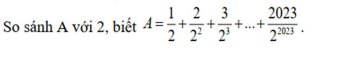
 giúp mình b) Câu 8 nhó
giúp mình b) Câu 8 nhó
2B:
a) C1: \(\dfrac{-7}{12}=\dfrac{-6-1}{12}=\dfrac{-6}{12}+\dfrac{-1}{12}=\dfrac{-1}{2}+\dfrac{-1}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{-3-4}{12}=\dfrac{-3}{12}+\dfrac{-4}{12}=\dfrac{-1}{4}+\dfrac{-1}{3}\)
C4: \(\dfrac{-7}{12}=\dfrac{-2-5}{12}=\dfrac{-2}{12}+\dfrac{-5}{12}\)
b) C1: \(\dfrac{-7}{12}=\dfrac{4-11}{12}=\dfrac{4}{12}-\dfrac{11}{12}=\dfrac{1}{3}-\dfrac{11}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{2-9}{12}=\dfrac{2}{12}-\dfrac{9}{12}=\dfrac{1}{6}-\dfrac{3}{4}\)
C3: \(\dfrac{-7}{12}=\dfrac{3-10}{12}=\dfrac{3}{12}-\dfrac{10}{12}=\dfrac{1}{4}-\dfrac{5}{6}\)