mik cần trong 1p nữa cứu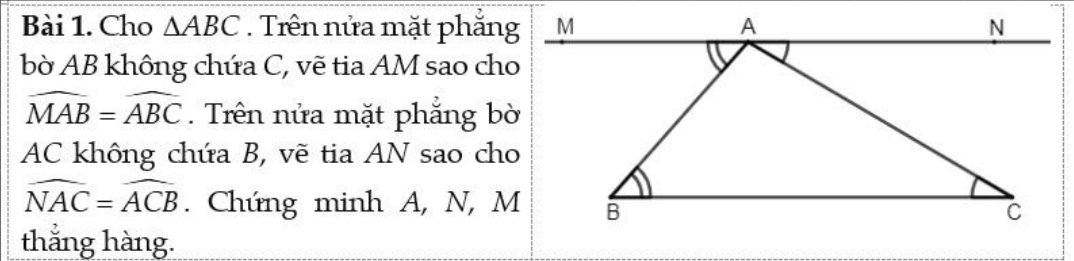
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
Gọi giá tiền mỗi chiếc áo bạn Hoa đã mua là x(nghìn đồng)
(Điều kiện: x>0)
Giá tiền ban đầu của mỗi chiếc áo là x+30(nghìn đồng)
Số lượng áo dự định là \(\dfrac{600}{x+30}\)(cái)
Số lượng áo thực tế là \(\dfrac{600}{x}\)(cái)
Vì số lượng áo thực tế mua được bằng 1,25 lần số lượng áo ban đầu định mua thì \(\dfrac{600}{x}=1,25\cdot\dfrac{600}{x+30}\)
=>\(\dfrac{600}{x}=\dfrac{750}{x+30}\)
=>\(\dfrac{4}{x}=\dfrac{5}{x+30}\)
=>5x=4x+120
=>x=120(nhận)
Vậy: Giá tiền của mỗi chiếc áo thực tế là 120 nghìn đồng


a: \(\left(-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}\right)-\left(\dfrac{3}{5}-\dfrac{1}{3}-\dfrac{3}{4}\right)\)
\(=-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}-\dfrac{3}{5}+\dfrac{1}{3}+\dfrac{3}{4}\)
\(=\left(-\dfrac{2}{5}-\dfrac{3}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)\)
=-1-1+1=-1
b: \(\dfrac{2}{5}-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(-\dfrac{1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{2}{5}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\left(\dfrac{2}{5}-\dfrac{4}{5}+\dfrac{2}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{9}+\dfrac{11}{9}\right)\)
\(=0+\left(-\dfrac{4}{3}+\dfrac{12}{9}\right)=0\)
c: \(\dfrac{11}{8}\cdot\left[\left(-\dfrac{5}{11}:\dfrac{13}{8}-\dfrac{5}{11}:\dfrac{13}{5}\right)+\dfrac{-6}{33}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\cdot\dfrac{8}{13}-\dfrac{5}{11}\cdot\dfrac{5}{13}-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\left(\dfrac{8}{13}+\dfrac{5}{13}\right)-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left(-\dfrac{5}{11}-\dfrac{2}{11}\right)+\dfrac{3}{4}=\dfrac{-7}{8}+\dfrac{3}{4}=-\dfrac{1}{8}\)
d: \(A=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)+\dfrac{4}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)+\dfrac{4}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\dfrac{-9}{15}+\dfrac{4}{9}:\dfrac{-3}{22}\)
\(=\dfrac{4}{9}\cdot\dfrac{-5}{3}+\dfrac{4}{9}\cdot\dfrac{-22}{3}=\dfrac{4}{9}\cdot\left(-\dfrac{5}{3}-\dfrac{22}{3}\right)=\dfrac{4}{9}\left(-9\right)=-4\)

a: Sửa đề; OA<OB
Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
=>AD=BC
b: Ta có: ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB};\widehat{ODA}=\widehat{OBC}\)
Ta có: OA+AB=OB
OC+CD=OD
mà OA=OC và OB=OD
nên AB=CD
Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(hai góc kề bù)
\(\widehat{OCB}+\widehat{DCB}=180^0\)
mà \(\widehat{OAD}=\widehat{OCB}\)
nên \(\widehat{DAB}=\widehat{DCB}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có:ΔEAB=ΔECD
=>EB=ED; EA=EC
Xét ΔOEB và ΔOED có
OE chung
OB=OD
EB=ED
Do đó: ΔOEB=ΔOED
=>\(\widehat{BOE}=\widehat{DOE}\)
=>OE là phân giác của góc xOy

Xét ΔABC có
HB,HC lần lượt là hình chiếu của AB,AC trên BC
AB=AC
Do đó: HB=HC

Để buộc 6 gói quà Lan cần dùng số mét dây lụa là:
\(\dfrac{3}{4}\times6=\dfrac{9}{2}\) ( m )
Đáp số: \(\dfrac{9}{2}\) m dây lụa

(-5,1)^2 - (-5,1).4,9
= (-5,1).(-5,1) - (-5,1).4,9
= (-5,1). (-5,1 - 4,9)
= (-5,1). -10
= 51
6,5 .13 + 0,35.130
= 6,5 .13 + 0,35.10.13
= 6,5 .13 + 3,5.13
=(6,5 + 3,5).13
= 10.13
= 130

\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
\(B=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{97\cdot99}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{97\cdot99}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{99}\right)=\dfrac{1}{2}\cdot\dfrac{98}{99}=\dfrac{49}{99}\)

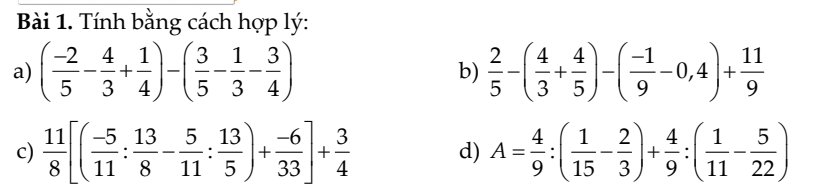
Ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MA//BC
Ta có: \(\widehat{NAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NA//BC
Ta có: MA//BC
NA//BC
MA,NA có điểm chung là A
Do đó: M,A,N thẳng hàng